HP 15c - Manual (Page 169)

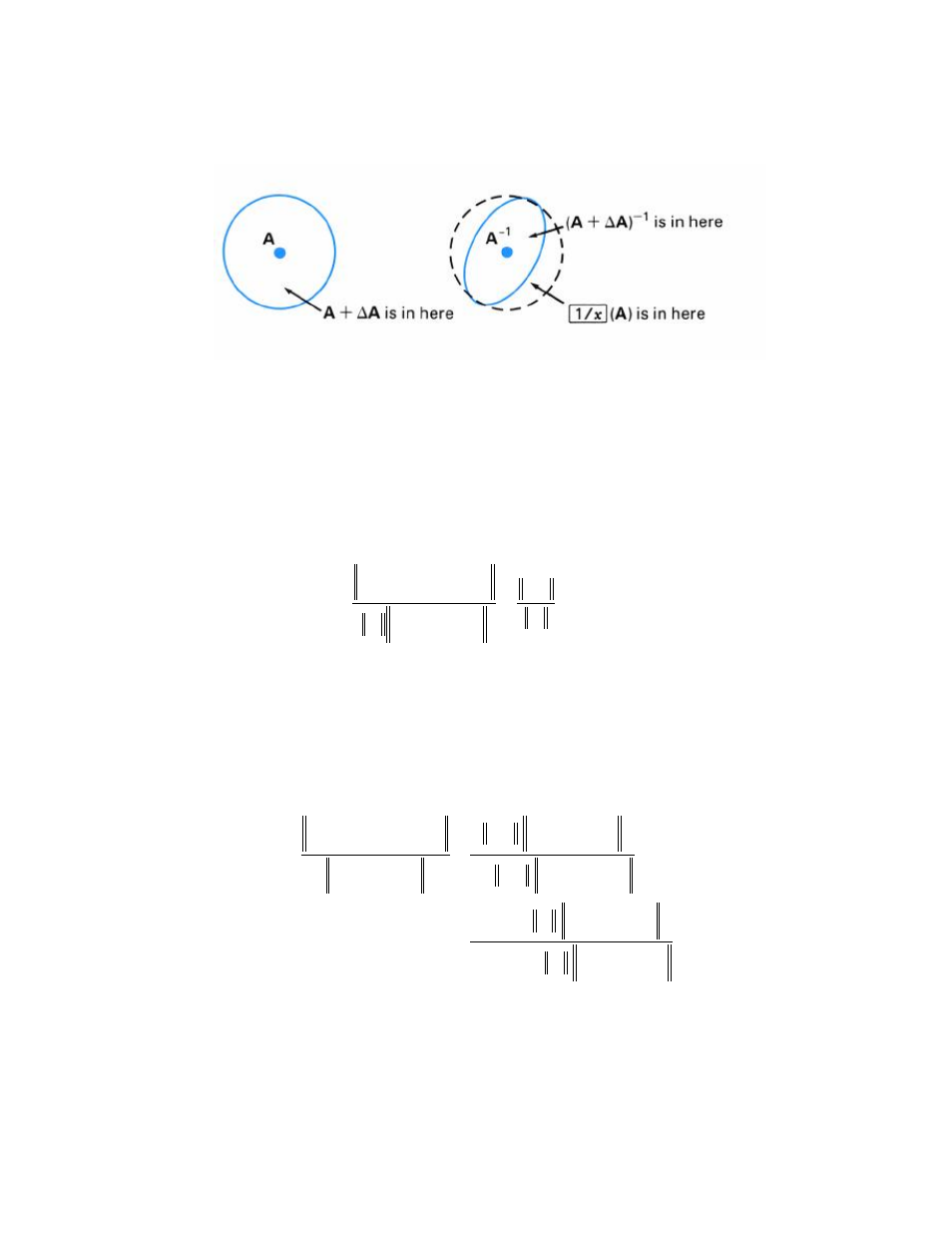
Appendix: Accuracy of Numerical Calculations 169
(A + ΔA)
-1
is at least about as far from A
-1
in norm as the calculated ⁄ (A). The figure
below illustrates the situation.
As A + ΔA runs through matrices with ||ΔA|| at least about as large as roundoff in ||A||, its
inverse (A + ΔA)
-1
must roam at least about as far from A
-1
as the distance from A
-1
to the
computed ⁄ (A). All these excursions are very small unless A is too near a singular
matrix, in which case the matrix should be preconditioned away from near singularity. (Refer
to section 4.)
If among those neighboring matrices A + ΔA lurk some that are singular, then many (A +
ΔA)
-1
and ⁄ (A) may differ utterly from A
-1
. However, the residual norm will always be
relatively small:
.
9
10
1
) (
1
) (
n

 





A
ΔA
ΔA
A A
I
ΔA
A A
This last inequality remains true when ⁄ (A) replaces (A + ΔA)
-1
.
If A is far enough from singularity that all
1/||(A + ΔA)
-1
|| > 10
-9
n ||A|| ≥ ||ΔA||,
then also
.
1
) (
9
10 1
1
) (
9
10
1
) ( 1
1
) (
1
) (
1
) (
1









 






 
ΔA A A
ΔA A A
ΔA
A
ΔA
ΔA
A
ΔA
ΔA
A
ΔA
A A
n
n
-
This inequality also remains true when ⁄ (A) replaces (A + ΔA)
-1
, and then everything on
the right-hand side can be calculated, so the error in ⁄ (A) cannot exceed a knowable
amount. In other words, the radius of the dashed ball in the figure above can be calculated.
The estimate above tend to be pessimistic. However, to show why nothing much better is true
in general, consider the matrix