HP 15c - Manual (Page 62)

62 Section 3: Calculating in Complex Mode
62
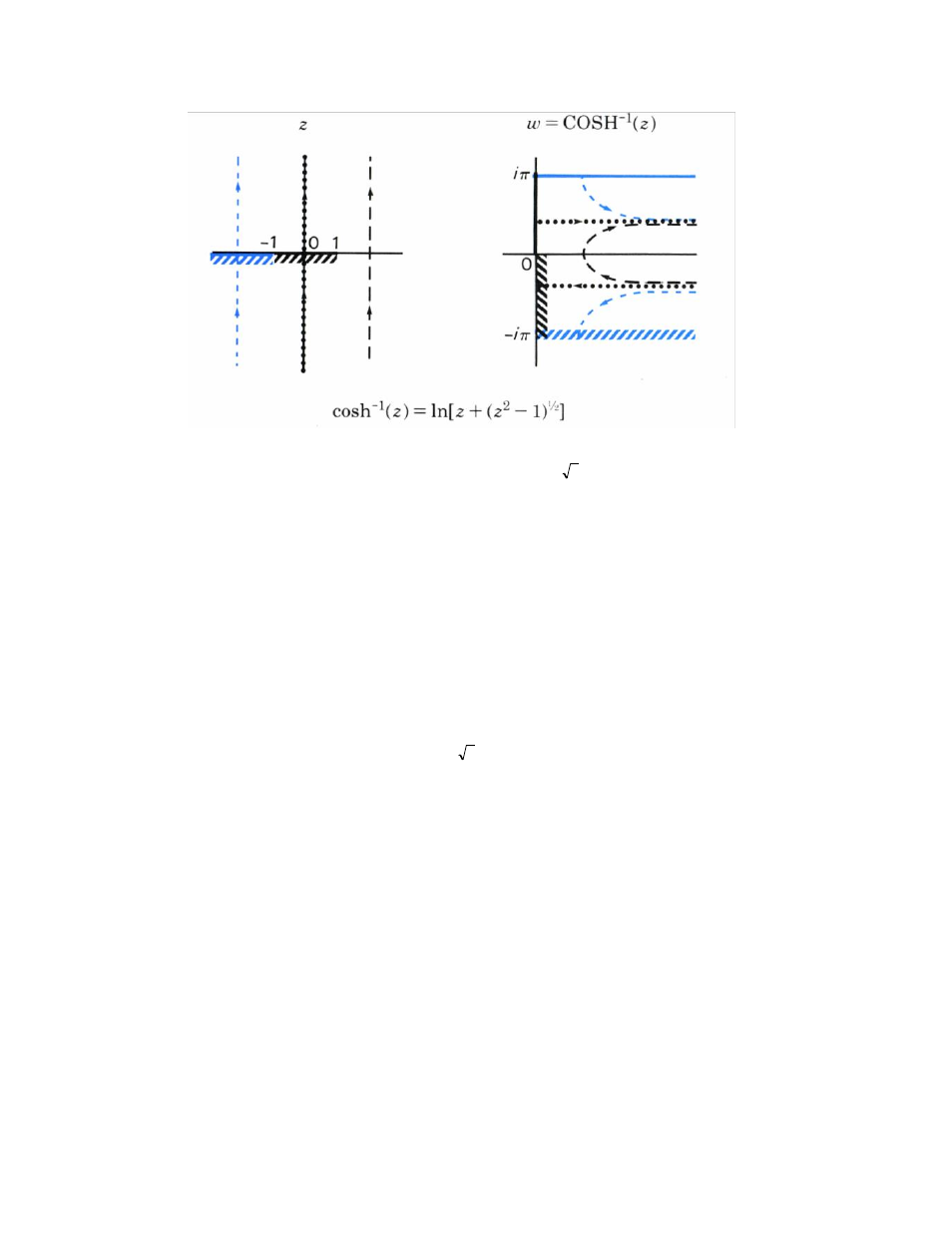
The principal branches in the last four graphs above are obtained from the equations shown,
but don't necessarily use the principal branches of ln(z) and
z
.
The remaining inverse functions may be determined from the illustrations above and the
following equations:
LOG(z) = LN(z) / LN(10)
SINH
−1
(z) = −i SIN
−1
(iz)
TANH
−1
(z) = −i TAN
−1
(iz)
w
z
= e
z LN(w)
.
To determine all values of an inverse relation, use the following expressions to derive these
values from the principal value calculated by the HP-15C. In these expressions, k= 0, ±1, ±2,
... .
z
½
= ±
z
ln(z) = LN(z) + i2kπ
sin
-1
(z) = (−1)
k
SIN
-1
(z) + kπ
cos
-1
(z) = ±COS
-1
(z) + 2kπ
tan
-1
(z) = TAN
-1
(z) + kπ
sinh
-1
(z) = (−1)
k
SINH
-1
(z) + ikπ
cosh
-1
(z) = ±COSH
-1
(z) + i2kπ
tanh
-1
(z) = TANH
-1
(z) + ikπ
w
z
= w
z
e
i2πkz
.