Theory – PASCO OS-8542 BLACK BODY LIGHT SOURCE User Manual
Page 6
Black Body Instruction Manual
012-07105B
2
GAIN
10
100
1
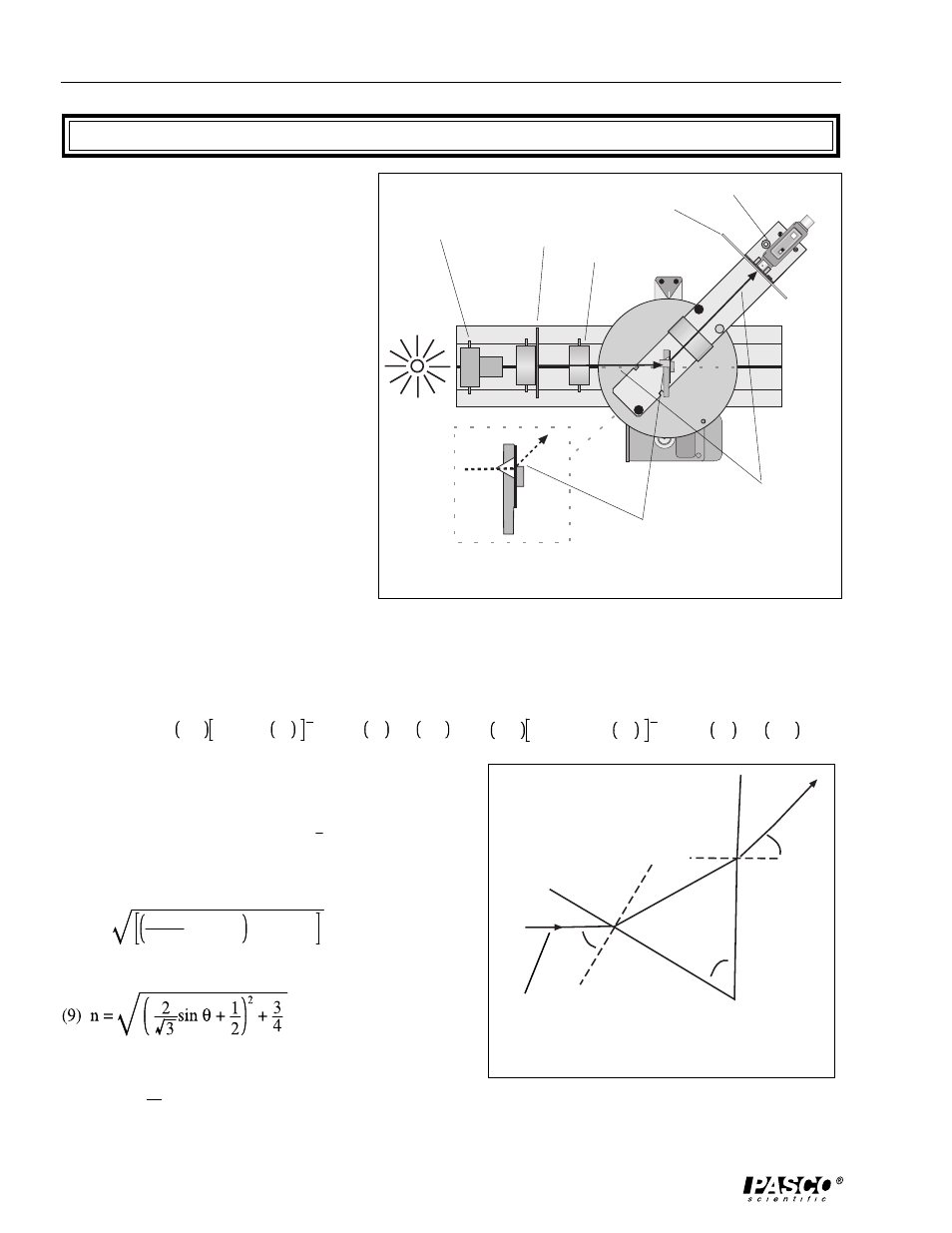
The 60-degree prism is mounted so that the
back face is perpendicular to the incoming
light, as shown in Figure 1. A schematic of
the prism and the path of light is shown in
Figure 2 below. Since the prism angle is 60
degrees, it can be shown that
(1)
θ
2
+
θ
3
= 60
°
And using Snell’s law at each interface,
(2) sin (60
°) = n sin (θ
2
) and
(3) sin (
θ) = n sin(θ
3
)
Combining equations (3) and (1) yields
(4) sin (
θ) = n sin (60° – θ
2
)
which, using the double angle formula
becomes
(5) sin (
θ) = n{ sin (60°) cos (θ
2
) – sin (
θ
2
) cos (60
°)}
Figure 1: Path of Light Through the Prism
Spectrophotometer
Theory
black body light
collimating slits
collimating lens
light sensor
aperture slits
prism mount
with prism
direction of light
Now use a trig identity to change from cos to sin, and (5) becomes
(6) sin
θ = n sin 60° 1 – sin
2
θ
2
1
2
– n sin
θ
2
cos 60
°
= sin 60° n
2
– n
2
sin
2
θ
2
1
2
– n sin
θ
2
cos 60
°
If we now use (2), equation 6 becomes
(7) sin(
θ) = sin(60°)[n
2
– sin
2
(60
°)]
1
2
– sin(60
°)cos(60°)
Solving (7) for n gives
(8) n =
sin
θ
sin60
+ cos60
2
+ sin
2
60
And finally, if we simplify,
The Cauchy equation gives the relationship between the
wavelength and the index of refraction.
(10) n(
λ) =
A
λ
2
+ B
where A and B depend on the type of glass.
Figure 2: Schematic of a Prism
n
path of light
θ
2
θ
θ
3
60°
60°
