National Instruments NI MATRIXx Xmath User Manual
Page 57
Chapter 3
Multiplicative Error Reduction
© National Instruments Corporation
3-11
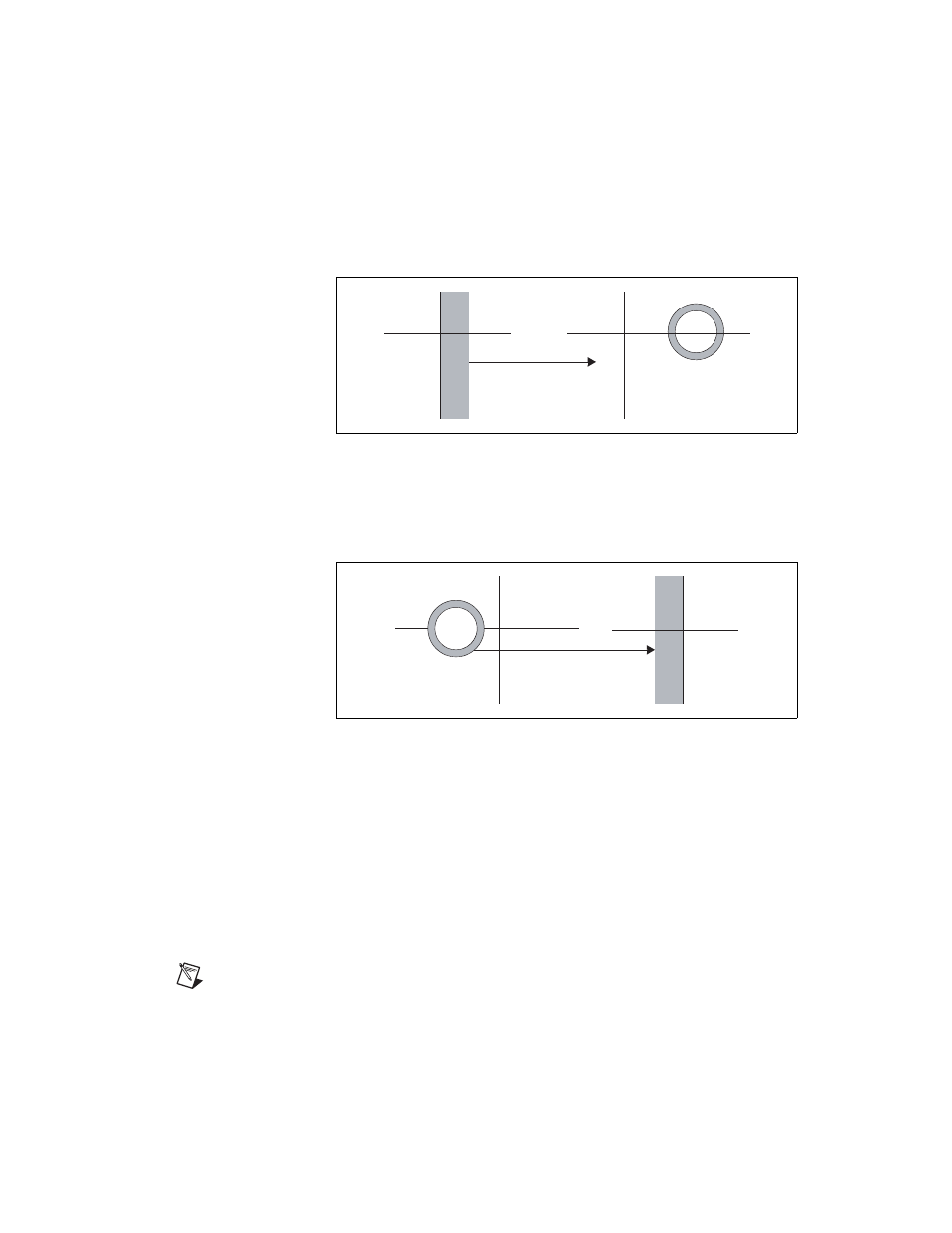
The values of G(s), as shown in Figure 3-2, along the j
ω-axis are
the same as the values of
around a circle with diameter defined by
[a – j0, b
–1
+ j0] on the positive real axis.
Figure 3-2. Bilinear Mapping from G(s) to
(Case 1)
Also, the values of
, as shown in Figure 3-3, along the j
ω-axis are
the same as the values of G(s) around a circle with diameter defined by
[–b
–1
+ j0, –a + j0].
Figure 3-3. Bilinear Mapping from G(s) to
(Case 2)
We can implement an arbitrary bilinear transform using the
subsys( )
function, which substitutes a given transfer function for the s- or z-domain
operator.
To implement
use:
gtildesys=subsys(gsys,makep([-b,1]/makep([1,-a])
To implement
use:
gsys=subsys(gtildesys,makep([b,1]/makep([1,a])
Note
The systems substituted in the previous calls to subsys invert the function
specification because these functions use backward polynomial rotation.
G˜ s
( )
G
˜ s
( )
G s
( )
values
values
a
b
1
–
G˜s
(
)
G˜ s
( )
G
˜ s
( )
G s
( )
values
values
-a
b
1
–
G˜s
(
)
G˜ s
( )
G
s a
–
bs
–
1
+
-------------------
⎝
⎠
⎛
⎞
=
G s
( )
G˜
s a
+
s 1
+
-----------
⎝
⎠
⎛
⎞
=
