Table 2-1. orders of g – National Instruments NI MATRIXx Xmath User Manual
Page 39
Chapter 2
Additive Error Reduction
2-16
ni.com
By abuse of notation, when we say that G is reduced to a certain order, this
corresponds to the order of G
r
(s) alone; the unstable part of G
u
(s) of the
approximation is most frequently thrown away. The number of eliminated
states (retaining G
u
) refers to:
(# of states in G) – (# of states in G
r
) – (# of states in G
u
)
This number is always the multiplicity of a Hankel singular value. Thus,
when the order of G
r
is n
i – 1
the number of eliminated states is n
i
– n
i – 1
or
the multiplicity of
σ
n
i – 1
+ 1
=
σ
ni
.
For each order n
i – 1
of G
r
(s), it is possible to find G
r
and G
u
so that:
(Choosing i = 1 causes G
r
to be of order zero; identify n
0
= 0.) Actually,
among all “approximations” of G(s) with stable part restricted to having
degree n
i – 1
and with no restriction on the degree of the unstable part, one
can never obtain a lower bound on the approximation error than
σ
n
i
; in the
scalar or SISO G(s) case, the G
r
(s) which achieves the previous bound is
unique, while in the matrix or MIMO G(s) case, the G
r
(s) which achieves
the previous bound may not be unique [Glo84]. The algorithm we use to
find G
r
(s) and G
u
(s) however allows no user choice, and delivers a single
pair of transfer function matrices.
The transfer function matrix G
r
( j
ω) alone can be regarded as a stable
approximation of G( j
ω). If the D matrix in G
r
( j
ω) is approximately
chosen, (and the algorithm ensures that it is), then:
(2-3)
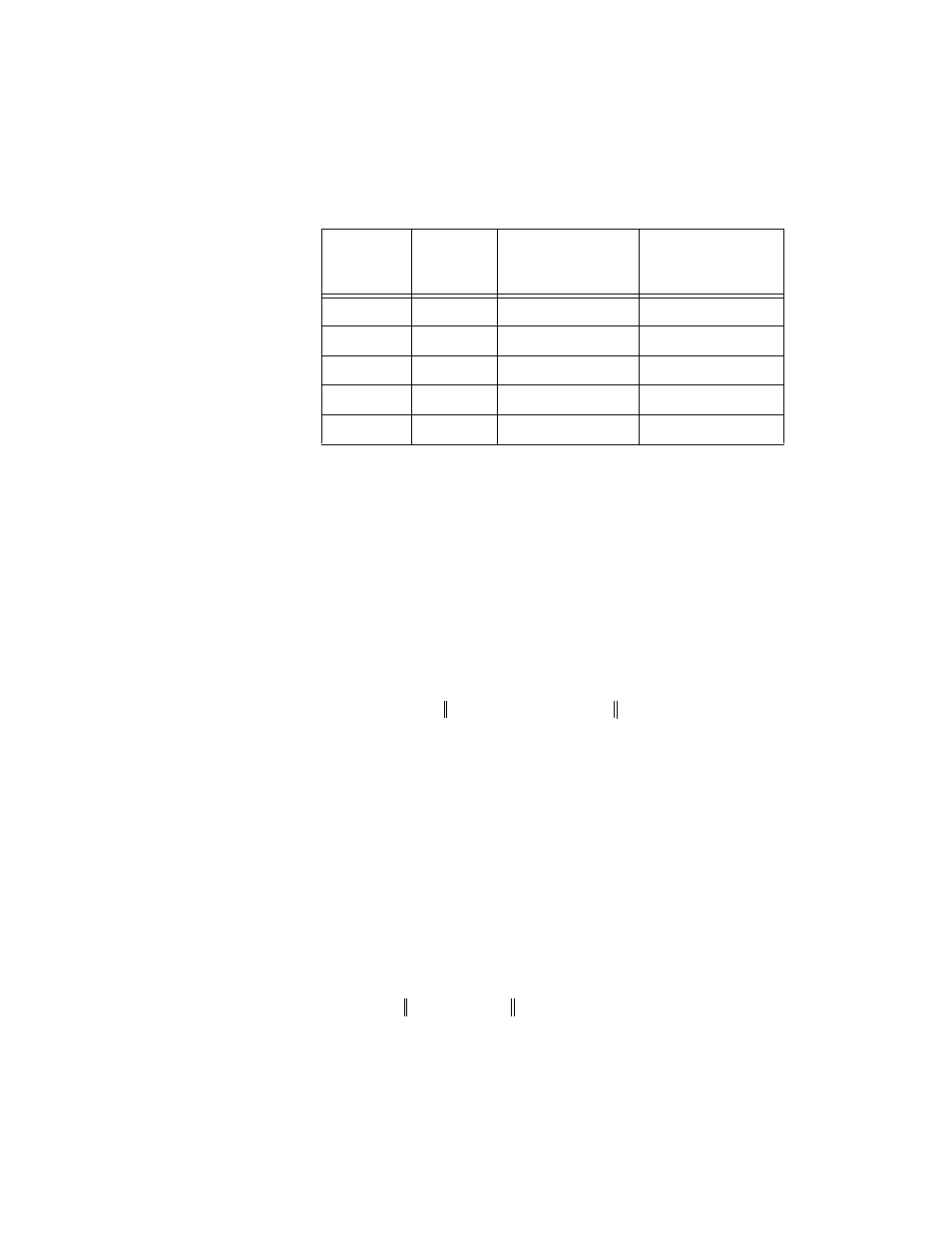
Table 2-1. Orders of G
Order of
G
r
nsr
Order of
G
u
nsu
Number of
Eliminated States
(Retaining G
u
)
Number of
Eliminated States
(Discarding G
u
)
0
ns – n
1
n
1
ns
n
1
ns – n
2
n
2
– n
1
ns – n
1
n
2
ns – n
3
n
3
– n
2
ns – n
2
⇓
⇓
⇓
⇓
n
m – 1
0
ns – n
m – 1
ns – n
m – 1
G j
ω
( ) G
r
j
ω
( )
–
G
u
j
ω
( )
–
∞
σ
n
i
≤
G j
ω
( ) G
r
j
ω
( )
–
∞
σ
n
i
σ
n
i 1
+
...
σ
ns
+
+
+
≤
