Kipp&Zonen LAS MkII Scintillometer User Manual
Page 72
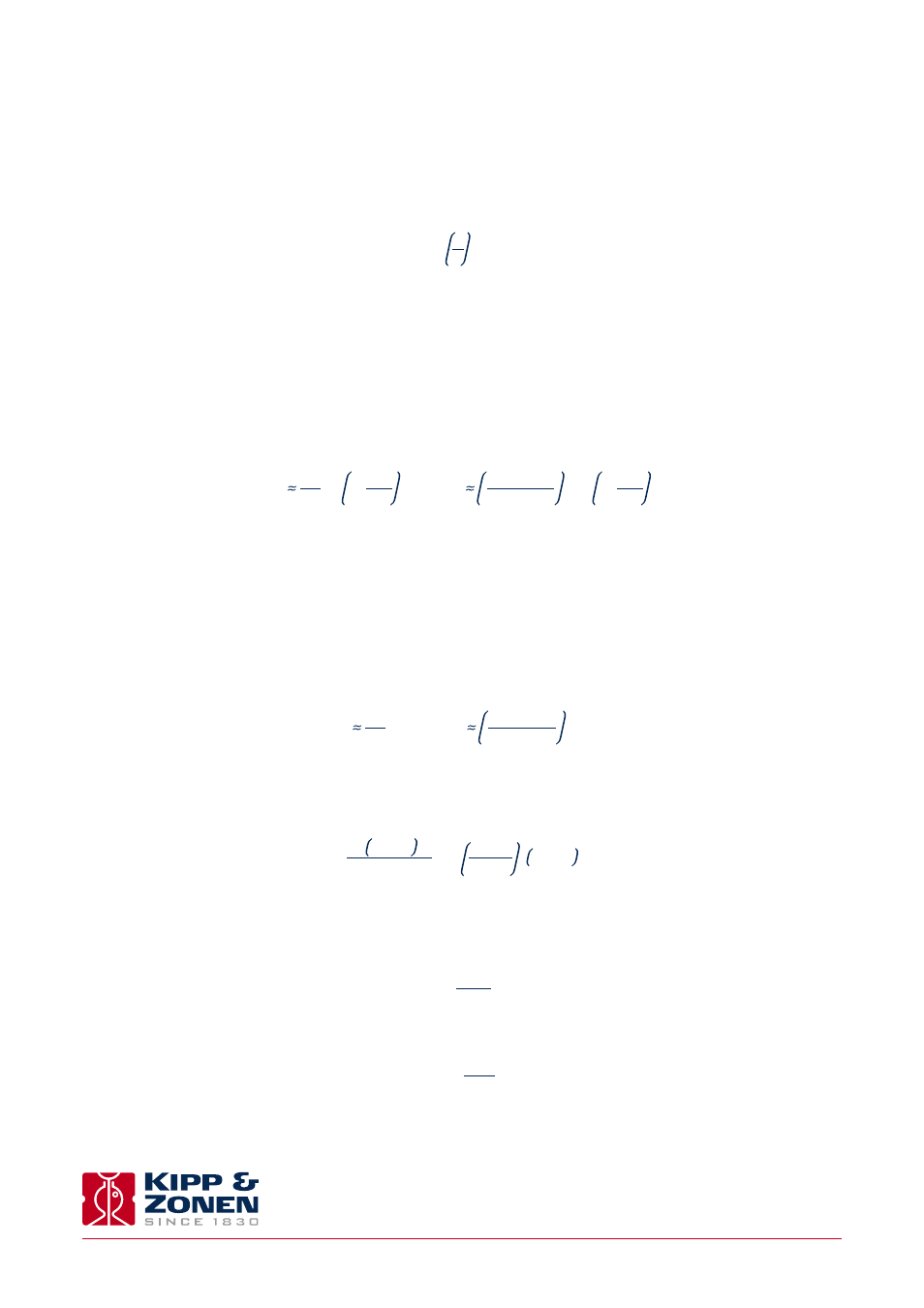
72
Instruction Manual - LAS MkII Scintillometer
.
When an electro-magnetic (EM) beam of radiation propagates through the atmosphere it is distorted by a number of processes.
These processes remove energy from the beam and lead to attenuation of the signal. The most serious mechanism that
influences the propagation of EM radiation is small fluctuations in the refractive index of the air (
n). These refractive index
fluctuations lead to intensity fluctuations, which are known as scintillations.
A scintillometer is an instrument that can measure the ‘amount’ of scintillations by transmitting a beam of light over a horizontal
path. The scintillations ‘seen’ by the receiving part of the instrument can be expressed as the structure parameter of the refractive
index of air (
C
n
2
), which is a representation of the ‘turbulent strength’ of the atmosphere. The turbulent strength describes the
ability of the atmosphere to transport scalars, such as heat, humidity and other species (dust particles, atmospheric gases).
For a Large Aperture Scintillometer, such as the LAS MkII, with equal transmitting and receiving apertures the relationship
between the measured variance of the natural logarithm of intensity fluctuations (
σ
lnI
2
) and the structure parameter is as follows
(Wang et al., 1978):
where
D is the aperture diameter of the LAS MkII and L the distance between the transmitter and the receiver (i.e. the path
length). Typical values of
C
n
2
lie between 10
-13
and 10
-18
m
-2/3
.
The graph below shows an example of the diurnal cycle of the structure parameter of the refractive index of air (
C
n
2
) derived from
a LAS MkII on a sunny day with a path length of 4.4 km and an effective height of 40 m.
The
C
n
2
values show a distinct drop around 6:00 and 18:00, sunrise and sunset, respectively. Around sunrise the atmosphere
changes from stable to unstable conditions and around sunset the atmosphere changes back from unstable to stable conditions.
In the atmosphere fluctuations in temperature (
T), humidity (Q), and (to a lesser extent) pressure (P), cause air density fluctuations
and with it fluctuations in the refractive index of air (
n). Therefore the structure parameter of the refractive index, C
n
2
, can be
decomposed into the structure parameters of temperature
C
T
2
, humidity
C
Q
2
, and the covariant term
C
TQ
as follows (neglecting
pressure fluctuations) (Hill et al., 1980):
.
A
T
and
A
Q
are functions of the beam wavelength and the mean values of temperature, absolute humidity, and atmospheric pressure
and thus represent the relative contribution of each term to
C
n
2
. In the visible and near-infrared wavelength region of the EM
spectrum
A
T
and
A
Q
are defined as follows (Andreas, 1988):
where
R
v
is the specific gas constant for water vapour (461.5 J K
-1
kg
-1
). Typical values for
A
T
and
A
Q
, for ‘normal atmospheric’
conditions (
P = 1⋅105 Pa, T = 288 K and Q = 0.012 kg m
-3
), are -0.27⋅10
-3
and -0.70⋅10
-6
, respectively. Because
A
T
is much larger
than
A
Q
the contribution of humidity related scintillations is much smaller than temperature related scintillations, i.e. the near-
infrared LAS MkII is primarily sensitive to temperature related scintillations. Therefore a simplified expression can be derived,
which makes it possible to derive
C
T
2
from
C
n
2
as follows (Wesley, 1976):
where
β is the Bowen ratio, which is a correction term for humidity related scintillations. The Bowen ratio is defined as the ratio
between the sensible heat flux (
H) and latent heat flux (L
v
E), i.e. β = H/L
v
E. When the surface conditions are dry H is larger than
L
v
E, resulting in high β values (> 3). This means that the correction term in the latter equation is small. Over wet surfaces β is
small (< 0.5), which means that a significant amount of scintillations are caused by humidity fluctuations, resulting in a large
correction.
Thus, when the surface conditions are very dry,
C
T
2
is directly proportional to
C
n
2
when
C
T
2
is known, the sensible heat flux (H) can be derived from similarity relationships that have been derived for
C
T
2
which
are based on the Monin-Obukhov Similarity Theory (MOST) (Wyngaard et al., 1971):
where d is the zero-displacement height and
z
LAS MkII
is the effective height of the scintillometer beam above the surface
(Hartogensis et al., 2003). T
*
is a temperature scale defined as:
and
L
MO
is the Obukhov length:
.
where
ρ is the density of air (~1.2 kg m
-3
),
c
p
the specific heat of air at constant pressure (~1005 J kg
-1
K
-1
),
k
v
the von Kármán
constant (~0.40), g the gravitational acceleration (~9.81 m s
-2
) and
u
*
the friction velocity. The universal stability function
f
T
is
defined as follows for unstable (day-time,
L
MO
< 0) conditions:
where
c
T1
= 4.9 and
c
T2
= 6.1,
and for stable (night-time,
L
MO
< 0) conditions as:
where
c
T3
= 2.2 (see Andreas, 1988; De Bruin et al., 1993; Wyngaard et al., 1971).
In order to derive H from
c
T2
, the friction velocity (
u
*
) is required. The friction velocity can be obtained from additional wind
speed data (
u) and an estimate of the surface roughness (z
0
) (Panofsky and Dutton, 1984):
where
z
u
is the height at which the wind speed is measured and
Ψ
m
is the integrated stability function for momentum defined as
(for unstable day-time conditions):
with:
and for (stable night-time conditions):
In summary, from
C
n
2
data together with wind speed, temperature, and an estimate of the surface roughness and the displacement
height, the sensible heat flux can be determined from the above equations, which can be solved iteratively.
.
For most day-time (unstable) conditions and when the LAS MkII is installed relatively high above the surface (
z
LAS MkII
> 20 m) the
contribution of the friction velocity is relatively small. For these conditions the free convection method can be applied:
where
b is an empirical constant:
This free convection approach provides a simpler method to determine
H (in this case termed ‘H
free
’) directly from
C
T2
without
knowing
u
*
. In practical applications the free convection approach can provide reasonably accurate fluxes under unstable
conditions (day-time) when the scintillometer is installed relatively high above the surface (
z
LAS MkII
> 20 m), as shown in the
figure below.
.
Summary of the steps to derive surface sensible heat flux,
H, from LAS MkII measurements:
Summary of the steps to derive free convection sensible heat flux,
H
free
, from LAS MkII measurements:
.
Finally, when additional net radiation (Q
*
) and soil heat flux (G
s
) data are available, the latent heat flux L
v
E
(or actual evaporation)
can be estimated applying the surface energy balance equation:
Below is an example of a time series of net radiation, soil heat flux, sensible heat flux and latent heat flux measurements.
Complete list of required data/information for deriving sensible heat flux (H):
• Mean of C
n
2
(derived from U
C
n
2
)
• Mean of signal strength (or U
demod
)
• Variance of signal strength (or U
demod
)
• Path length (L)
• Average (effective) beam height (z
LAS MkII
)
• Zero-displacement height (d)
• Air pressure (P)
• Air temperature (T)
• Wind speed (u)
• Bowen ratio (β)
• Height(s) of cup anemometer(s) (z
u
)
• Surface roughness length of source area for LAS MkII and wind speed measurements (z
o
)
Additional data required for deriving latent heat flux (L
v
E
):
• Net radiation
• Soil heat flux
Other useful meteorological data:
• Wind direction
• Rainfall
T
P
A
T
=
-0.78⋅10
-6
+0.126⋅10
-6
R
V
Q
A
Q
=
-0.126⋅10
-6
R
V
Q
or
T
2
β
A
T
2
2
0.03
C
n
2
C
T
2
1+
β
2
0.03
C
T
2
1+
T
2
2
-0.78⋅10
-6
P
C
n
2
or
T
2
A
T
2
C
n
2
C
T
2
C
T
2
T
2
2
-0.78⋅10
-6
P
C
n
2
=
L
MO
f
T
T
*
2
C
T
2
2/3
z
LAS
- d
z
LAS
- d
L
MO
< 0
T
*
=
-H
ρ
c
p
u
*
L
MO
=
u
*
2
T
gk
v
T
*
