PASCO SP-9268A STUDENT SPECTROMETER - Manual (Page 10)

6
Student Spectrometer 012-02135F
¨
9. Repeat steps 6-8 until the angles for the correspond-
ing slit images are the same to within one minute of
arc.
Making the Reading
Once the grating is aligned, do not rotate the rotating
table or its base again. Diffraction angles are measured
as described in the previous section, Measuring Angles
of Diffraction. (Since the vernier scales were moved
when the spectrometer table was adjusted, the point of
zero diffraction must be remeasured).
Wavelengths are determined according to the formula:
l = a sin q
n
where
λ
is the wavelength; a is the distance between
lines on the diffraction grating
(a = 3.3 x 10
-3
mm for the 300 line/mm grating or
1.66 x 10
-3
mm for the optional 600 line/mm grating);
θ
is the angle of diffraction; and n is the order of the dif-
fraction spectrum under observation.
Using the Prism
Advantages and Disadvantages
A prism can also be used as the diffracting element in a
spectrometer since the index of refraction of the prism
(and therefore the angle of refraction of the light) varies
slightly depending on the wavelength of the light.
A prism refracts the light into a single spectrum, whereas
the grating divides the available light into several spec-
tra. Because of this, slit images formed using a prism are
generally brighter than those formed using a grating.
Spectral lines that are too dim to be seen with a grating
can often be seen using a prism.
Unfortunately, the increased brightness of the spectral
lines is offset by a decreased resolution, since the prism
doesn't separate the different lines as effectively as the
grating. However, the brighter lines allow a narrow slit
width to be used, which partially compensates for the
reduced resolution.
With a prism, the angle of refraction is not directly pro-
portional to the wavelength of the light. Therefore, to
measure wavelengths using a prism, a graph of wave-
length versus angle of refraction must be constructed us-
ing a light source with a known spectrum. The wave-
length of unknown spectral lines can then be interpo-
lated from the graph.
Once a calibration graph is created for the prism, future
wavelength determinations are valid only if they are
made with the prism aligned precisely as it was when the
graph was produced. To ensure that this alignment can
be reproduced, all measurements are made with the
prism aligned so that the light is refracted at the angle of
minimum deviation.
The Angle of Minimum Deviation
The angle of deviation for light traversing a prism is
shown in Figure 9. For a given wavelength of light tra-
versing a given prism, there is a characteristic angle of
incidence for which the angle of deviation is a minimum.
This angle depends only on the index of refraction of the
prism and the angle (labeled A in Figure 8) between the
two sides of the prism traversed by the light. The rela-
tionship between these variables is given by the equa-
tion:
sin
n =
{ }
A+D
2
sin A2
where n is the index of refraction of the prism; A is the
angle between the sides of the prism traversed by the light;
and D is the angle of minimum deviation. Since n varies
with wavelength, the angle of minimum deviation also var-
ies, but it is constant for any particular wavelength.
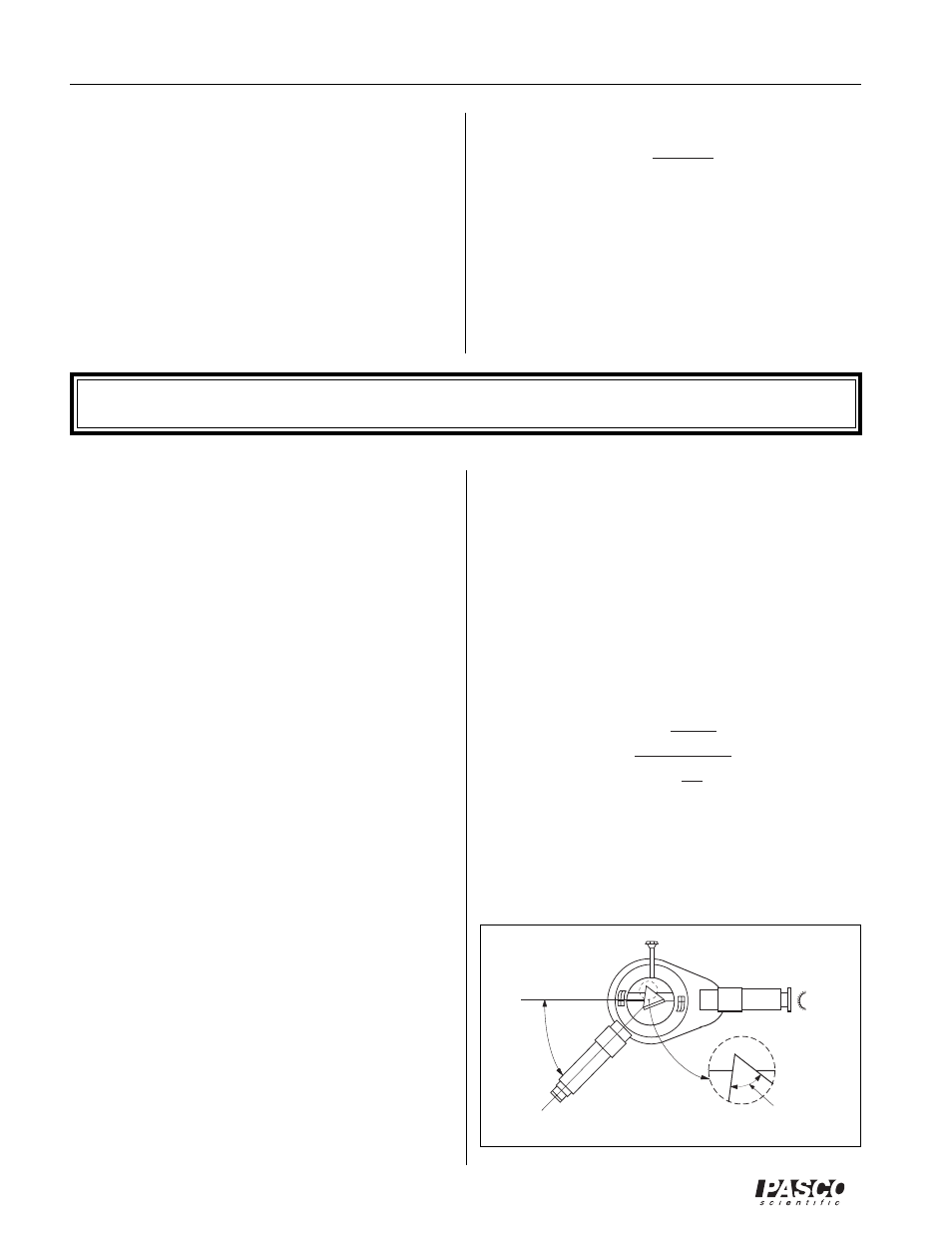
LIGHT
SOURCE
UNDEFLECTED
RAY
DEFLECTED
RAY
ANGLE OF
DEVIATION
ANGLE A
Figure 9 Angle of Deviation