PASCO ME-9426A AMUSEMENT PARK PHYSICS - Manual (Page 13)

012-03776E Amusement Park Physics
9
Objective
In this lab you will measure the maximum acceleration on a swing and compare this to a value arrived at through
the principles of conservation of energy and centripetal force.
Discussion
On a swing, we see a number of important physical phenomena, including simple harmonic motion, driven
harmonic motion, inertia, conversion of energy between gravitational potential and kinetic, and centripetal force.
In this experiment, we use the latter two ideas to calculate an acceleration and then compare the results with the
acceleration we actually measure. At least two people are needed to carry out this lab. They will need both a
horizontal and a vertical accelerometer.
Procedure
1. Person A begins swinging with the vertical accelerometer. Person B takes up a position to the side so that he/
she can see and measure the angle of the swinger’s motion.
2. Person A on the swing keeps the vertical accelerometer pointed upwards along the chain or rope, and will
focus on reading the maximum value as he/she passes through the bottom-most point of the swing. This value
will be recorded as a
max
.
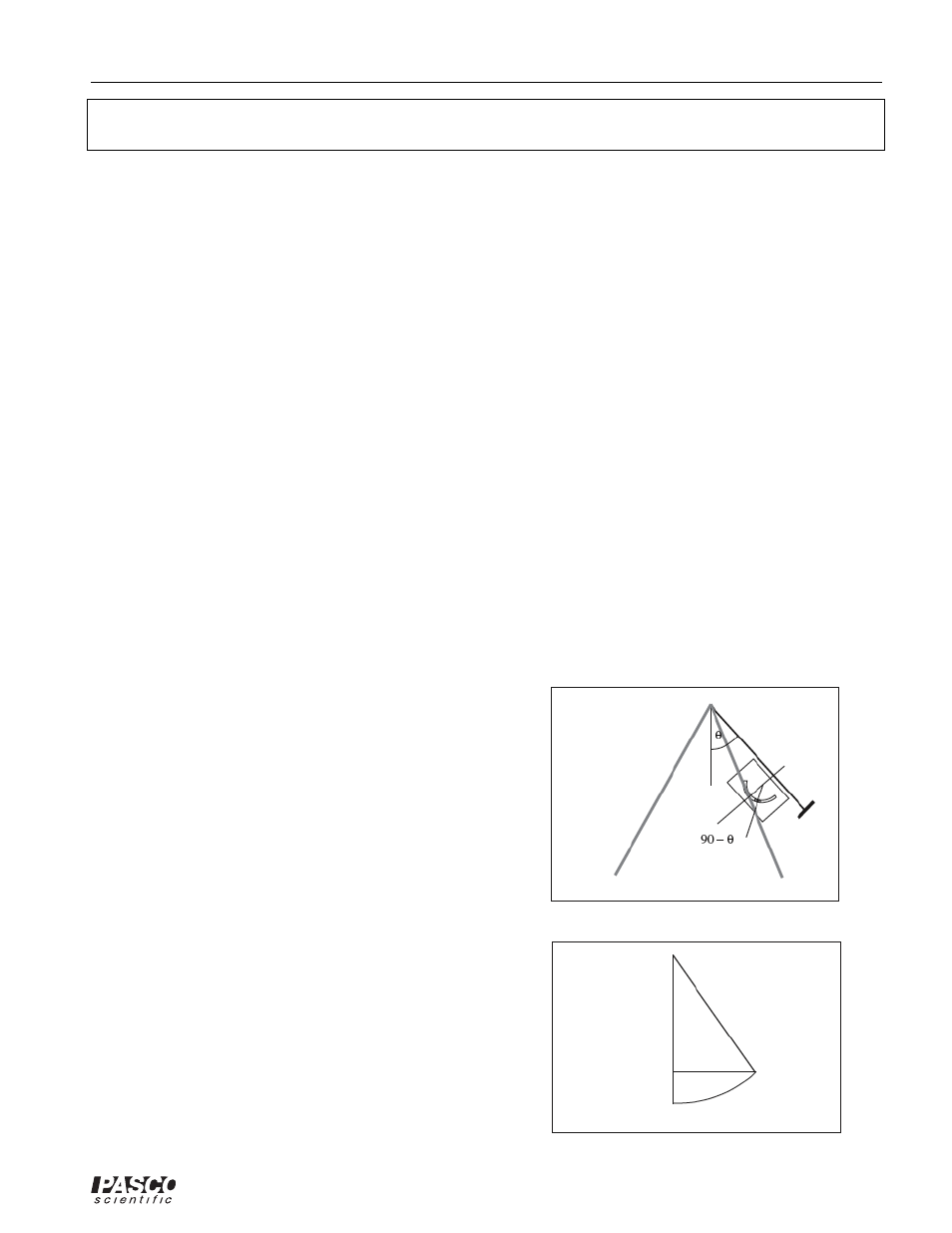
3. Person B, to the side, will use the lateral accelerometer to measure the maximum angle that the swinger moves
to during the swing. Line the straw side of the accelerometer up with the chain. The angle θ that is indicated
on the accelerometer is going to be 90° minus the angle from the vertical. The angle measured should be
recorded as well as its complement. See Figure 1.
4. When the person on the swing gets to a point where the observer on the ground has a good reading on the
maximum angle, write down both the angle and the maximum acceleration. Repeat in this manner for at least
three different angles, then change places and repeat. Use Table 3 to record your data.
5. Finally, determine the length of the swing. You can use one person’s
height and then scale up, or pace off a horizontal distance and use the
lateral accelerometer to determine the height, or use an appropriate
measuring device. With the swinger seated, you can approximate his/
her center of mass as being close to the seat.
Analysis
1. Use trigonometry as shown below to calculate the difference in heights
of the swinger between the maximum height and the bottom of the
swing for each trial. Record your calculations in Table 4. NOTE: This
value can actually be measured directly with a measuring tape by
pulling the swing back to the angle determined by person B.
2. Apply conservation of energy between gravitational potential (G.P.E.)
and kinetic (K.E.) to determine the maximum velocity at the bottom
of the swing. Note that the equations give mg
∆h = 1/2 mv 2 , so the
mass divides out.
3. The acceleration at the bottom of the swing has two parts: gravity and
centripetal. We can show that the centripetal acceleration is just v 2 /
L, where L is the length of the swing. Calculate this value and convert
to g’s by dividing your result by 9.8 m/sec
2 . Add the 1 g due to gravity
to get the total acceleration.
4. Compare the values you calculated and the corresponding values
Experiment 2: Playground Physics / The Swing
Figure 1
Figure 2
L
θ
L cos
θ
∆
h
∆
h = L - L cos
θ