PASCO WA-9867 Sine Wave Generator - Manual (Page 22)

Sine Wave Generator Resonance Tubes
22 ®
Part I:
Closed Tube of Variable Length
Theory
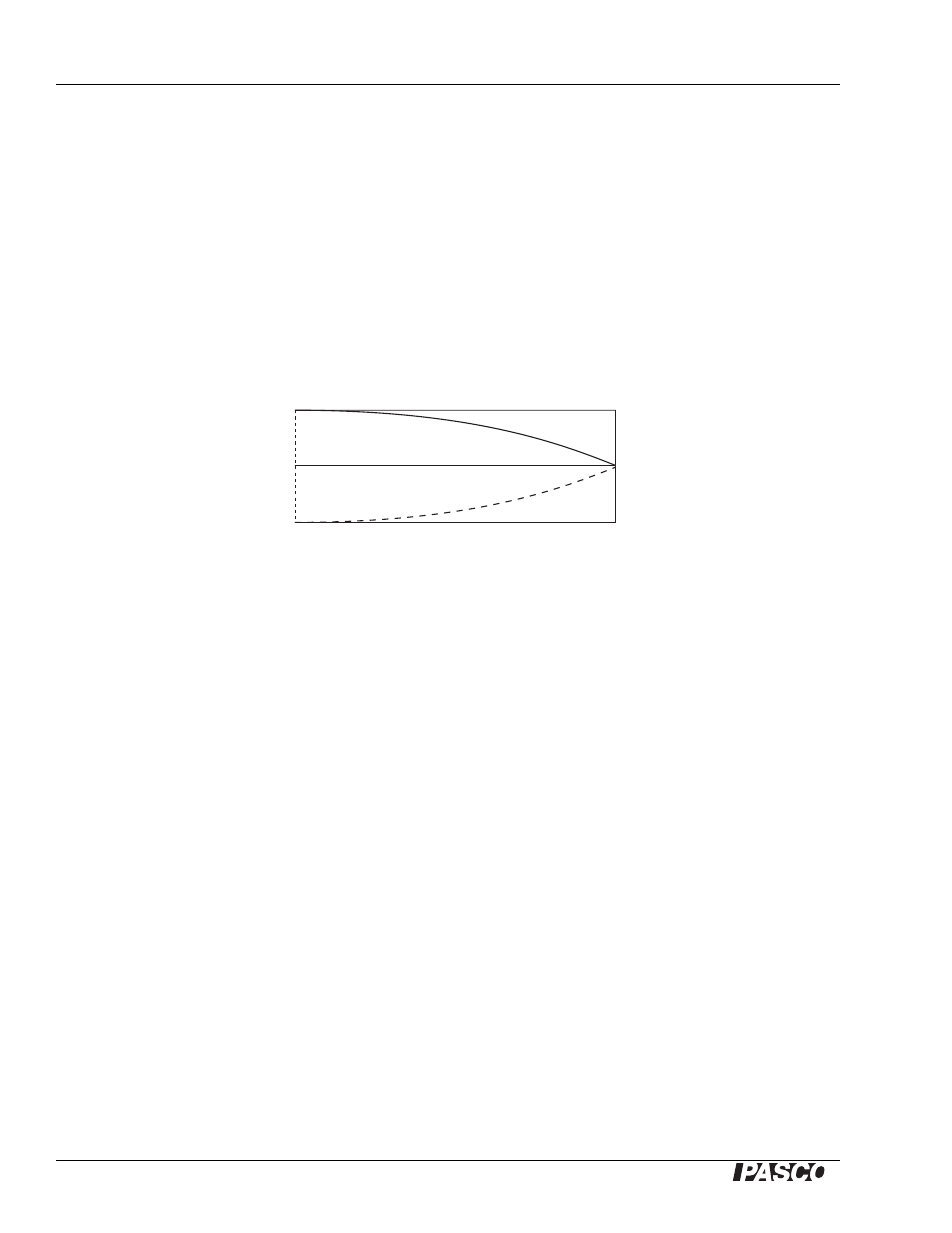
A resonating tube with one end open and the other end closed will always have a node at the
closed end and an anti-node at the open end. A node represents an area where the velocity of the
air is a minimum (zero), and an anti-node represents an area where the velocity of the air is a
maximum. If the tube is resonating in the fundamental mode (lowest possible frequency) it will
have no other nodes or anti-nodes. This is shown in the diagram below, where the curved lines
represent the velocity profile of the air in the tube.
On a sine wave, the distance from one of the maxima to the next point where it crosses zero is a
quarter wavelength. Thus, for a tube with one open end and one closed end, the length of the tube,
L, and the wavelength,
λ, are related by:
(eq. 1)
For all types of waves, the relationship between the frequency (f) and the velocity (v) of the wave
is:
(eq. 2)
For a resonating tube, v is the speed at which sound travels through the air in the tube, and f is the
frequency of the sound. In this experiment, the sound frequency is the frequency of the Sine Wave
Generator.
Combining equations 1 and 2 yields:
(eq. 3)
Thus we see that the length of the tube is inversely proportional to the fundamental frequency.
Procedure
1. Extend the tube so that the scale reads 100 cm (the white tube slides inside the blue tube). Use
a meter stick inside the tube to check if the scale is accurate. If the value is not correct within
0.2 cm, record the offset and compensate for this discrepancy in all future measurements.
Node
Closed End Open End
Antinode
λ 4L
=
v
λ f
=
L ¼ v
1
f
--- =