Sharp EL-9900 - Manual (Page 83)

8
Advanced Keyboard/CALCULUS USING THE SHARP EL-9900
Copyright © 2002, Sharp Electronics Corporation. Permission is granted to photocopy for educational use only.
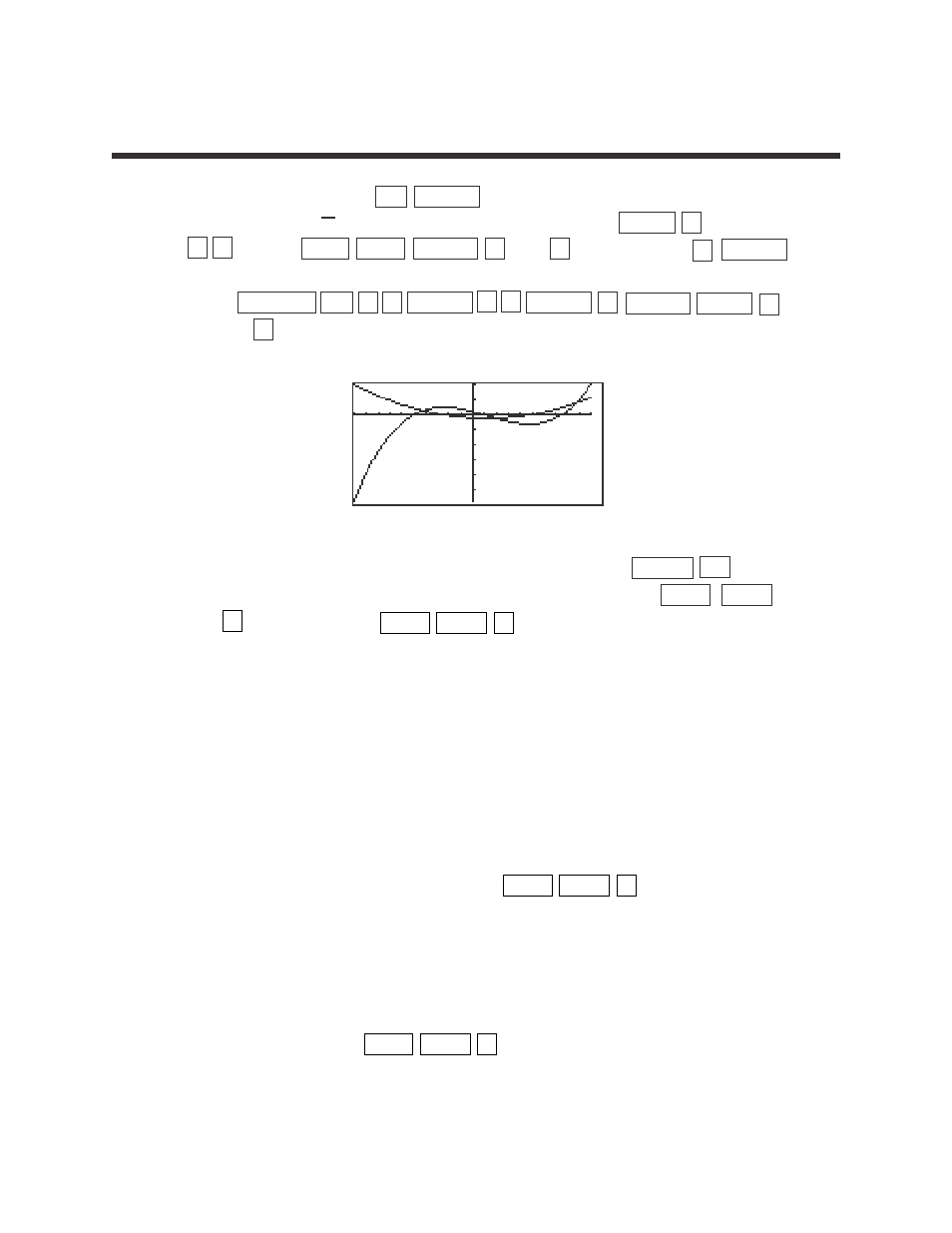
1. Graph f ’(x) by pressing Y= ENTER entering f(x)= 2x 3 – 7x 2 – 70x + 75 for
Y1, and entering (Y1) for Y2. Enter Y2 by pressing MATH A (CALC)
0 5 (d/dx ( ) 2ndF VARS ENTER A (XY) 1 (Y1) and press ) ENTER .
2. Press WINDOW (–) 1 0 ENTER 1 0 ENTER 1 ENTER ZOOM A
(Zoom) 1 (Auto) to obtain the graphs of f(x) and f ’(x).
3. We now want to find the two x-intercepts of f ’(x). Press TRACE
▼ to
place the tracer on the graph of the derivative. Then, press 2ndF CALC
and 5 (X_Incpt). Press 2ndF CALC 5 (X_Incpt) again to obtain the
other x-intercept.
4. Comparing these values to the x-coordinates of the points at which the
maxima and minima of f(x) occur, we see they are the same.
5. Where is f ’(x) positive? Notice this is where the graph of f(x) is increasing.
Where is f ’(x) negative? Notice this is where f(x) is decreasing.
6. Next, find the minimum point of f ’(x) by first making sure the trace cursor is
on the graph of the derivative, pressing 2ndF CALC 3 (Minimum).
7. Look at f(x) and observe that this appears to be the point at which the
function “bends a different way.”
8. Find the point of inflection directly by moving the cursor to the original
function and pressing 2ndF CALC 7 (Inflec).
GRAPHS OF DERIVATIVES
d
dx