HP 40gs User Manual
Page 302
16-28
Step-by-Step Examples
Solution 3
The calculator is not needed here. Simply stating that
increases for
is sufficient to yield the
inequality:
Solution 4
Since
is positive over [0, 2], through multiplication
we get:
and then, integrating:
Solution 5
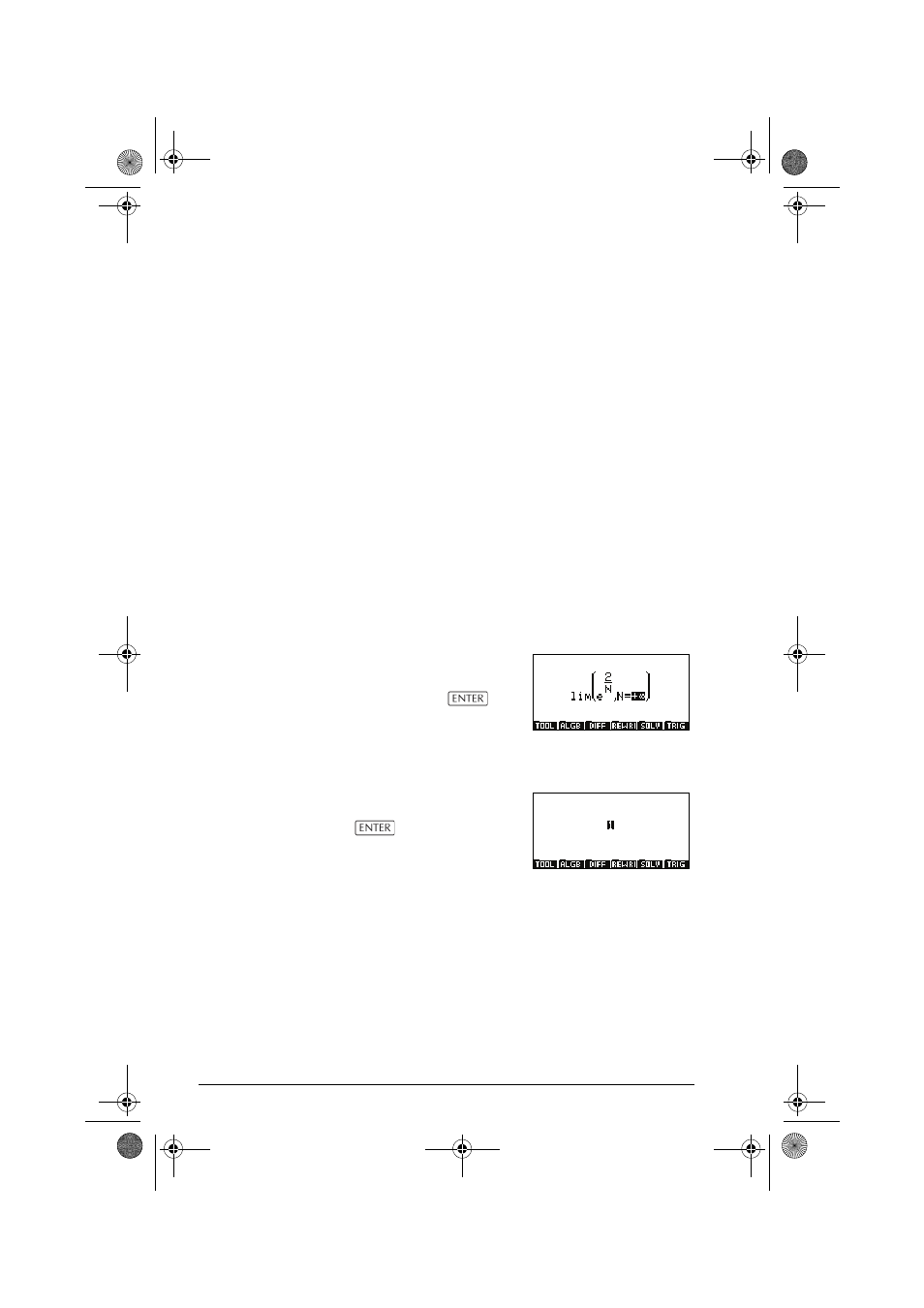
First find the limit of
when
→ + .
Note: pressing
after you have selected the
infinity sign from the
character map places a “+”
character in front of the infinity sign.
Selecting the entire
expression and pressing
yields:
1
In effect, tends to 0 as
tends to + , so
tends to
as tends to + .
As
tends
to
+ ,
is the portion between and a
quantity that tends to .
Hence,
converges, and its limit is .
We have therefore shown that:
e
x
n
---
x
0 2
[ , ]
∈
1 e
x
n
---
e
2
n
---
≤
≤
g x
( )
g x
( ) g x
( )e
x
n
---
g x
( )e
2
n
---
≤
≤
I u
n
e
2
n
---
I
≤
≤
e
2
n
---
n
∞
2
n
---
n
∞
e
2
n
---
e
0
1
=
n
∞
n
∞ u
n
I
I
u
n
I
L
I
4
2
ln
–
=
=
hp40g+.book Page 28 Friday, December 9, 2005 1:03 AM
