PASCO OS-8529 SLIT ACCESSORY - Manual (Page 9)

012–06348A Slit Accessory
5
Purpose
The purpose of this experiment is to examine the diffraction
and interference patterns formed by laser light passing
through two slits and verify that the positions of the maxima
in the interference pattern match the positions predicted by
theory.
Theory
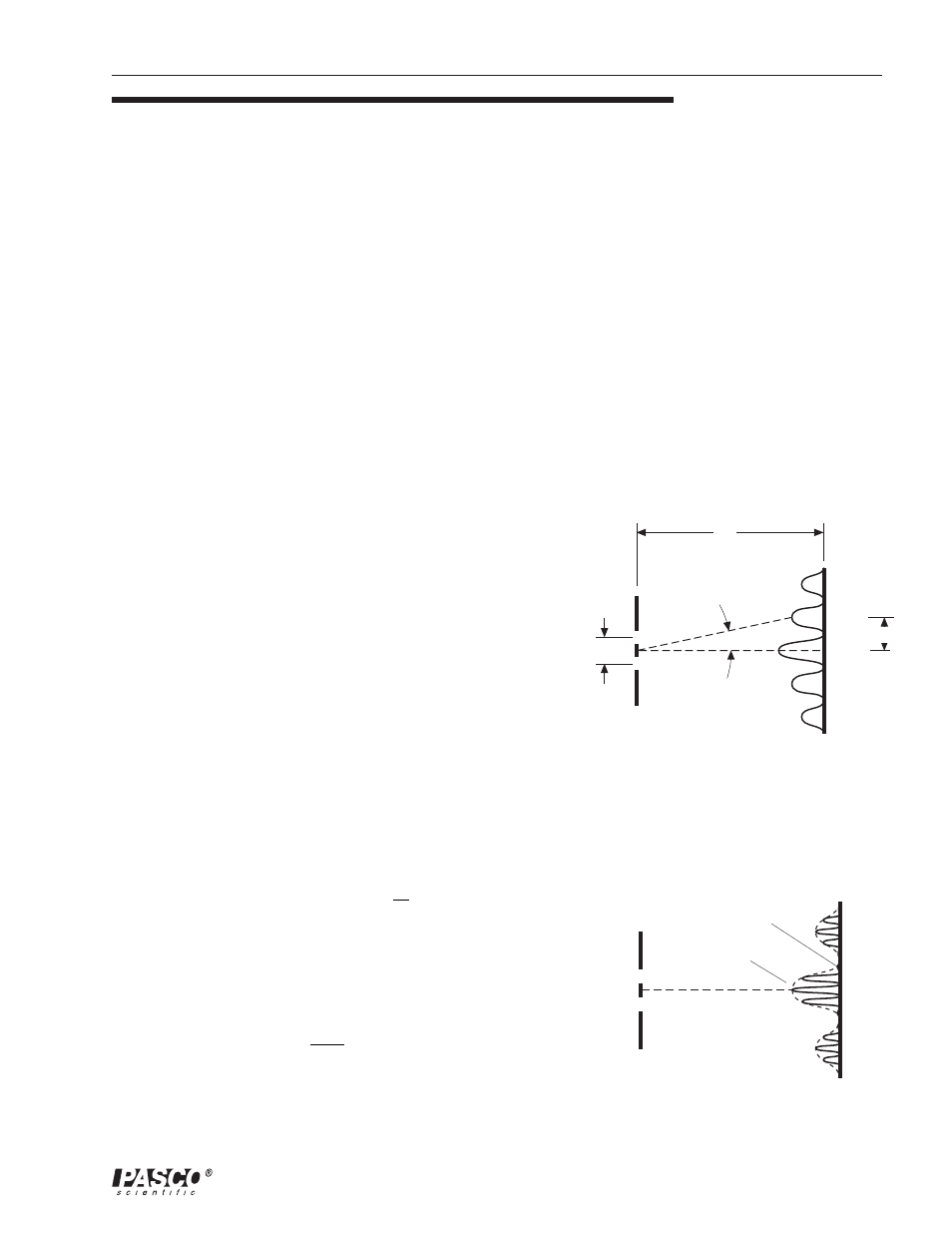
When light passes through two slits, the two light rays
emerging from the slits interfere with each other and
produce interference fringes. The angle to the maxima
(bright fringes) in the interference pattern is given by
where d is the slit separation, θ is the angle from the center
of the pattern to the m th maximum, λ is the wavelength of
the light, and m is the order (0 for the central maximum, 1
for the first side maximum, 2 for the second side maximum,
. . . counting from the center out). See Figure 2.1.
Since the angles are usually small, it can be assumed that
From trigonometry,
where y is the distance on the screen from the center of the
pattern to the m
th maximum and D is the distance from the
slits to the screen as shown in Figure 2.1. The interference
equation can thus be solved for the slit separation:
While the interference fringes are created by the interference
of the light coming from the two slits, there is also a
diffraction effect occurring at each slit due to single slit
diffraction, causing the envelope diagramed in Figure 2.2.
Experiment 2: Interference from a Double Slit
d sin θ = m λ (m = 0, 1, 2, 3 . . .)
sin θ ≅ tan θ
d =
m
λ
D
y
(m = 0, 1, 2, 3 . . .)
tan
θ
=
y
D
Figure 2.2: Single Slit Diffraction
Envelope
Materials required:
• optics bench 1 • white projection surface
• Diode Laser (OS-8528) • metric rule
• Multiple Slit Set (OS-8529) • page 2 of the Slit Accessory manual
1 From the Introductory or Advanced Optics System (OS-8500 or OS-9254A)
Figure 2.1: Interference Fringes
central envelope
dotted line is diffraction envelope
diffraction minimum
D
screen
slit
y
m = 1
m = 2
m = 2
m = 0
θ
d
m = 1
m = 1
m = 0
m = 2
m = 4
m = 3