PASCO ES-9070 COULOMB BALANCE - Manual (Page 14)

Coulomb Balance 012-03760E
10
Measuring the Charges, q
1
and q
2
Method I:
The capacitance of an isolated conductive sphere is given by the equation:
C = 4 p e
0
a;
where C is the capacitance, e
0
= 8.85 x 10 –12 F/m, and a = the radius of the sphere.
For a capacitor, charge (q) and charging potential (V) are related by the equation: q = CV. You can
use this equation to determine the charge on the spheres from your applied charging potential.
This is the simplest method for determining the charge on the spheres. Unfortunately, the conducting
spheres of the Coulomb Balance are not isolated in this application, so the measured values of q will
be only approximate.
ä NOTE: A capacitor normally consists of two conductors. The charge on one conductor is +q and
the charge on the other is –q. V is the potential difference between the two conductors. For an
isolated sphere with a charge +q, the second conductor is a hypothetical plane at ground potential
and with charge –q, located at a distance infinitely far from the sphere.
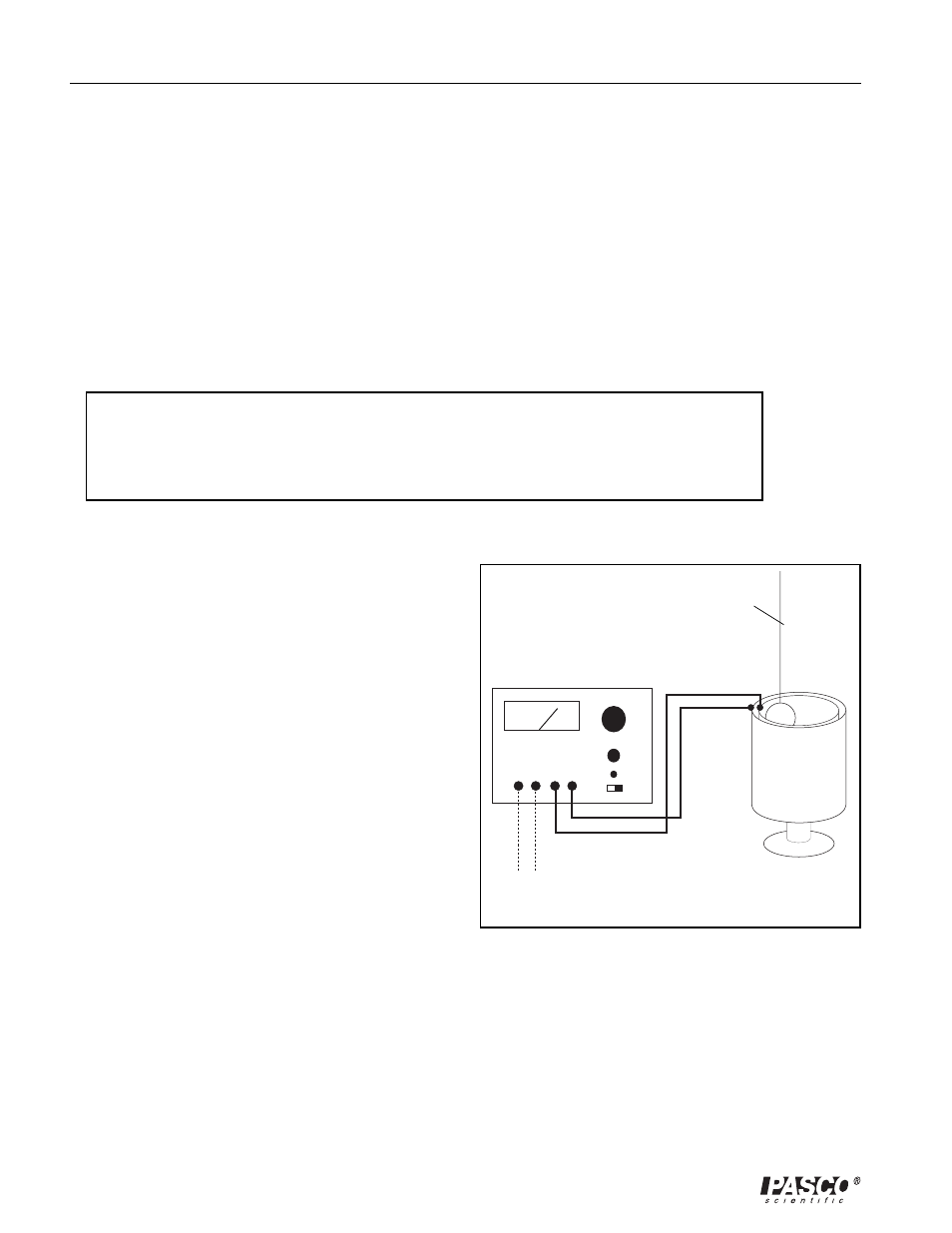
Method II:
The charge on the spheres can be measured more
accurately using an electrometer with a Faraday ice
pail. The setup for the measurement is shown in
Figure 8. The electrometer and ice pail can be
modeled as an infinite impedance voltmeter in
parallel with a capacitor. A sphere with a charge q is
touched against the ice pail. Since the capacitance of
the ice pail and electrometer is much greater than
that of the sphere, virtually all of the charge q is
transferred onto the ice pail. The relationship
between the voltage reading of the electrometer and
the charge deposited into the system is given by the
equation q = CV, where C is the combined capaci-
tance of the electrometer, the ice pail, and the
connecting leads. Therefore, in order to determine
the charge, you must know the capacitance of the
system.
The simplest way to measure the capacitance of the
electrometer and ice pail is to use a good capaci-
tance meter connected between the inside and
outside conductors of the ice pail (the electrometer
must be connected to the ice pail during the measurement). A second method is to charge a precision
capacitor with capacitance equal to C
test
(³ 250 pF) to a known voltage V
test
(10 - 30 V). The charge
on the capacitor is then equal to q
test
= C
test
V
test
. Place the leads of the charged capacitor between the
inside and outside conductors of the ice pail. The charge q
test
is now distributed across two parallel
capacitors, the precision capacitor and the capacitance of the ice pail and electrometer system.
Therefore: C
test
V
test
= (C + C
test
)V; where C is the capacitance of the electrometer and Faraday ice pail
and V is the voltage reading of the electrometer.
Figure 8. Measuring the Charge with an
Electrometer and a Faraday Ice Pail
Faraday
ice pail
Conductive sphere on an
insulating thread
Electrometer