PASCO ES-9070 COULOMB BALANCE - Manual (Page 11)

012-03760E Coulomb Balance
7
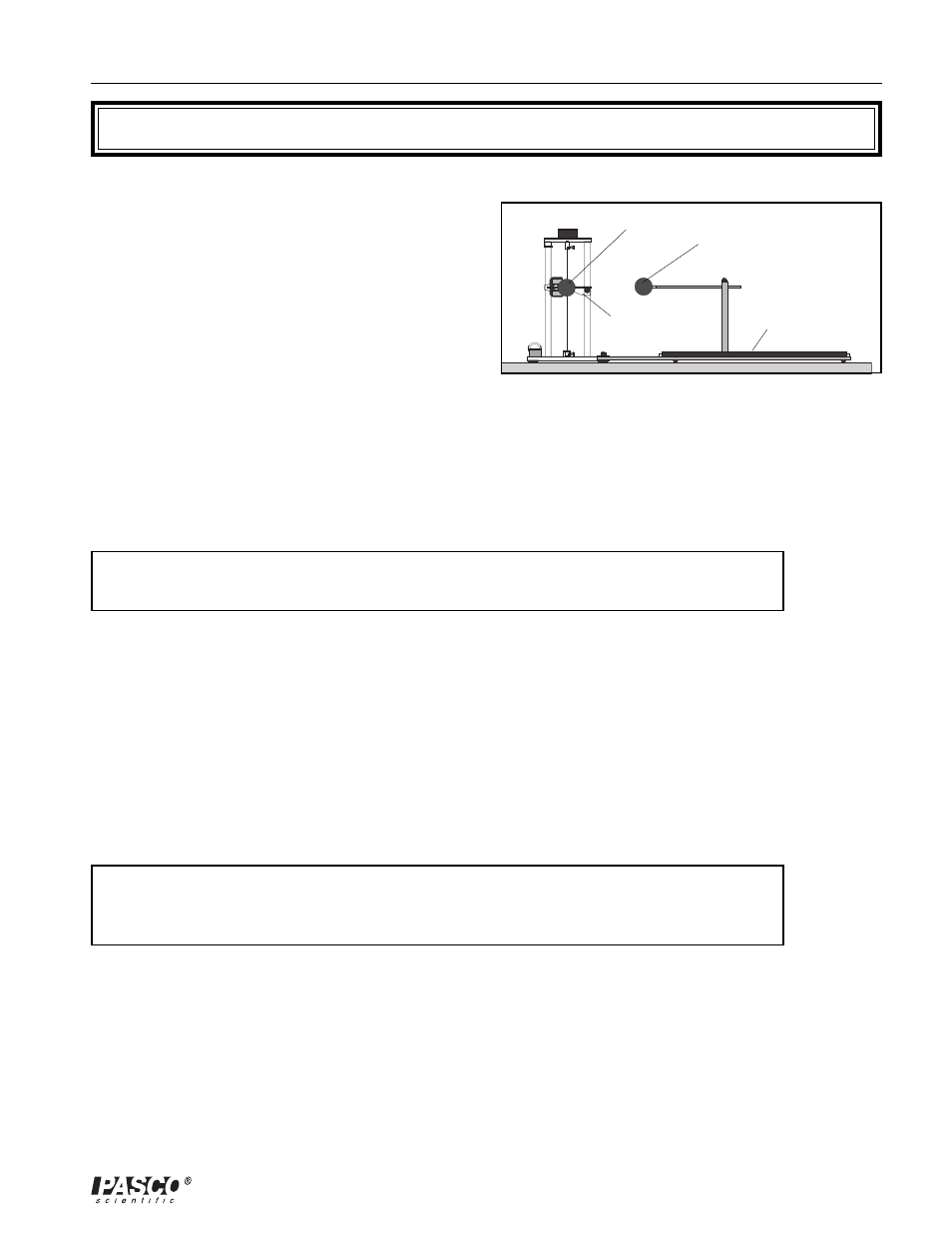
Experiment: (Part A) Force Versus Distance
suspended
sphere
sliding
sphere
slide assembly
pendulum
assembly
Procedure
➀ Set up the Coulomb Balance as described in the
previous section.
➁ Be sure the spheres are fully discharged (touch
them with a grounded probe) and move the sliding
sphere as far as possible from the suspended sphere.
Set the torsion dial to 0×C. Zero the torsion balance
by appropriately rotating the bottom torsion wire
retainer until the pendulum assembly is at its zero
displacement position as indicated by the index
marks.
➂ With the spheres still at maximum separation, charge both the spheres to a potential of
6-7 kV, using the charging probe. (One terminal of the power supply should be grounded.)
Immediately after charging the spheres, turn the power supply off to avoid high voltage leakage
effects.
ä IMPORTANT: Read the section Tips for Accurate Results. It has some helpful hints about
charging the spheres.
➃ Position the sliding sphere at a position of 20 cm. Adjust the torsion knob as necessary to balance
the forces and bring the pendulum back to the zero position. Record the distance (R) and the angle
(q) in Table 1.
➄ Separate the spheres to their maximum separation, recharge them to the same voltage, then
reposition the sliding sphere at a separation of 20 cm. Measure the torsion angle and record your
results again. Repeat this measurement several times, until your result is repeatable to within ± 1
degree. Record all your results.
➅ Repeat steps 3-5 for 14, 10, 9, 8, 7, 6 and 5 cm.
Analysis
ä NOTE: In this part of the experiment, we are assuming that force is proportional to the
torsion angle. If you perform Part C of the experiment, you will test this assumption when you
calibrate the torsion balance.
Determine the functional relationship between the force, which is proportional to the torsion angle
(q); and the distance (R). This can be done in the following ways:
➀ Plot log q versus log R.
Explanation: If q = bR
n , where b and n are unknown constants, then log q = n log R + log b.
The slope of the graph of log q versus log R will therefore be a straight line. Its slope will be equal
to n and its y – intercept will be equal to log b. Therefore, if the graph is a straight line, the
function is determined.
Figure 6. Experimental Setup