PASCO ME-6815 PROJECTILE CATCHER ACCESSORY - Manual (Page 19)

012-05091E Projectile Catcher Accessory
15
CAUTION! DO NOT LOOK DOWN BARREL! CAUTION! DO NOT LOOK DOWN BARREL! CAUTION! DO NOT LOOK DOWN THE BARREL.
LONG RANGE MEDIUM RANGE SHORT RANGE
Position of Ball
Launch
SHORT RANGE PROJECTILE LAUNCHER ME-6800
Yellow Band in Window Indicates Range. 9 0 8 0 7 0 6 0 5 0 4 0 3 0 2 0 1 0 0
WEAR SAFETY GLASSES WHEN IN USE.
Use 25 mm
balls ONLY!
DEMONSTRATION: Inelastic/Elastic Collisions
m
c
+ m
b
EQUIPMENT NEEDED
– Projectile Launcher (ME-6800)
– Projectile Catcher Accessory (ME-6815)
– Dynamics Track (ME-9435A)
– Dynamics Cart (ME-9430)
Purpose
The purpose of this demonstration is to show that the final cart speed during an elastic
collision between the steel ball and the cart is twice the final cart speed of that during
an inelastic collision between the steel ball and the cart.
Theory
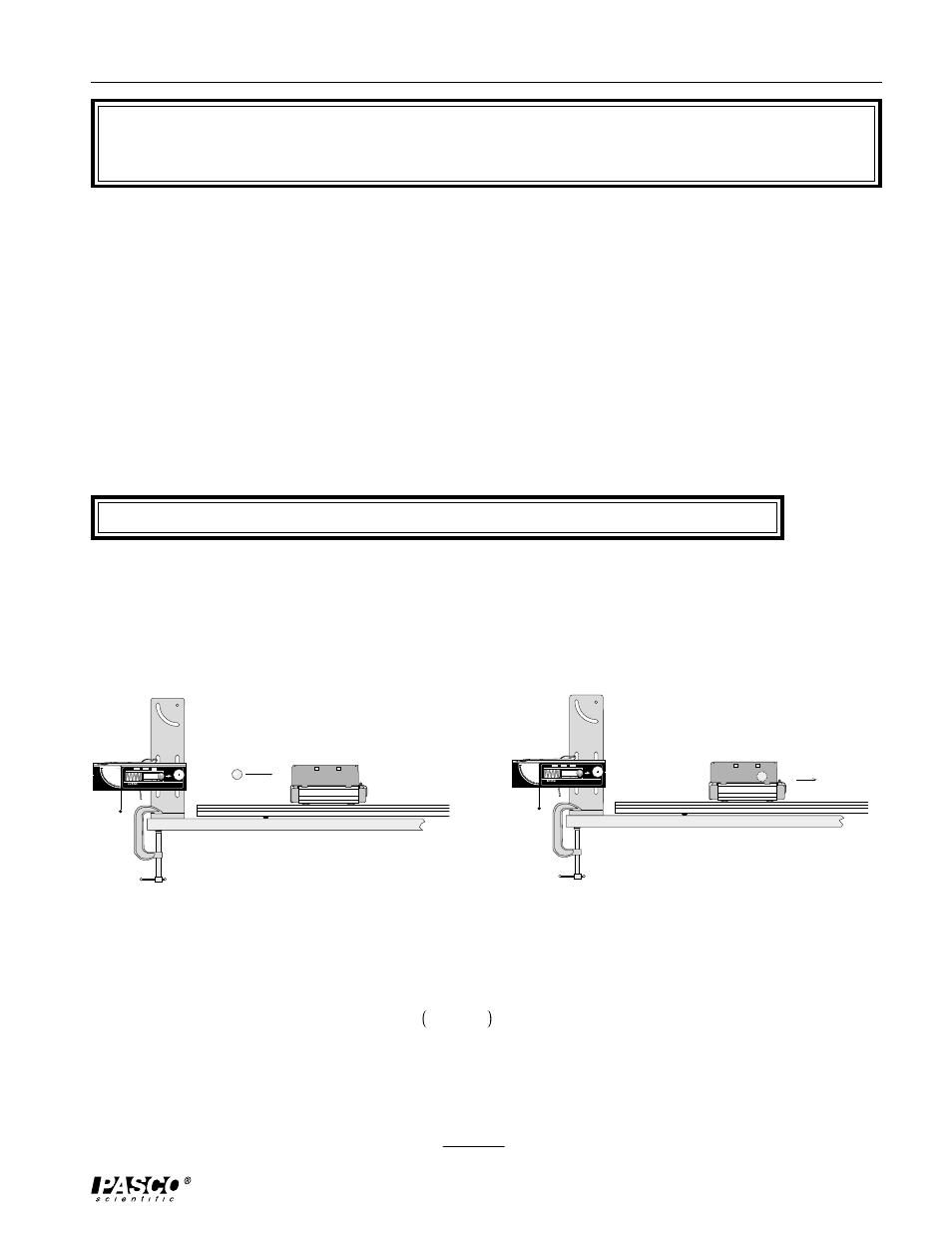
Inelastic Collision
A ball is launched horizontally and embeds in the catcher mounted on the dynamics
cart. The cart and ball then move off at a constant velocity. See Figure 3.1.
CAUTION! DO NOT LOOK DOWN BARREL! CAUTION! DO NOT LOOK DOWN BARREL! CAUTION! DO NOT LOOK DOWN THE BARREL.
LONG RANGE MEDIUM RANGE SHORT RANGE
Position of Ball
Launch
SHORT RANGE PROJECTILE LAUNCHER ME-6800
Yellow Band in Window Indicates Range. 9 0 8 0 7 0 6 0 5 0 4 0 3 0 2 0 1 0 0
WEAR SAFETY GLASSES WHEN IN USE.
Use 25 mm
balls ONLY!
Before Collision
Figure 3.1: Conservation of Momentum in the Inelastic Collision
m
b
v
o
m
c
v = o
v
c
After Collision
Momentum is conserved during the collision, but energy is not conserved. The mo-
mentum before the collision is equal to the momentum after the collision:
P
before
= P
after
m
b
v
o
= m
b
+ m
c
v
c
where m
b
is the mass of the ball, v
o
is the muzzle velocity of the ball, m
c
is the mass of
the catcher and cart, and v
c
is the velocity of the cart and ball immediately after the
collision. Solving for the final speed of the cart gives
v
c
=
m
b
m
b
+ m
c
v
o