PASCO ME-8949 EQUAL ARM BALANCE - Manual (Page 4)

4
Equal Arm Balance 012-05921A
®
EQUAL ARM BALANCE
MAXIMUM TOTAL MASS NOT TO EXCEED ONE KILOGRAM
P A S C O
s c i e n t i f i c
ME-8949
➂ Within the limits of uncertainty, what is the most plau-
sible mathematical relationship between
τ
and r , F ,
and
θ
?
Limited Warranty
PASCO scientific warrants this product to be free from
defects in materials and workmanship for a period of one
year from the date of shipment to the customer. PASCO
will repair or replace, at its option, any part of the product
which is deemed to be defective in material or workman-
ship. This warranty does not cover damage to the product
caused by abuse or improper use. Determination of
whether a product failure is the result of a manufacturing
defect or improper use by the customer shall be made
solely by PASCO scientific. Responsibility for the return
of equipment for warranty repair belongs to the customer.
Equipment must be properly packed to prevent damage
and shipped postage or freight prepaid. (Damage caused
by improper packing of the equipment for return ship-
ment will not be covered by the warranty.) Shipping
costs for returning the equipment, after repair, will be
paid by PASCO scientific.
This experiment has been adapted from Unit 13:
Angular Momentum and Torque as Vectors
Observation of Torque when F and r are not
Perpendicular
In Experiment 2, you “discovered” that if we define
torque as the product of a lever arm and perpendicular
force, an object does not rotate when the sum of the
torques acting on it add up to zero. However, we didn’t
consider cases where F and r are not perpendicular, and
we didn’t figure out a way to tell the direction of the rota-
tion resulting from a torque. Let’s consider these compli-
cations by generating torques with spring balances and an
Equal Arm Balance once more. For this activity you’ll need:
• 1 Equal Arm Balance
• 1 clamp stand (to hold the Balance)
• 2 spring scales, 5 N
• 1 ruler
• 1 protractor
Torque as a Function of Angle
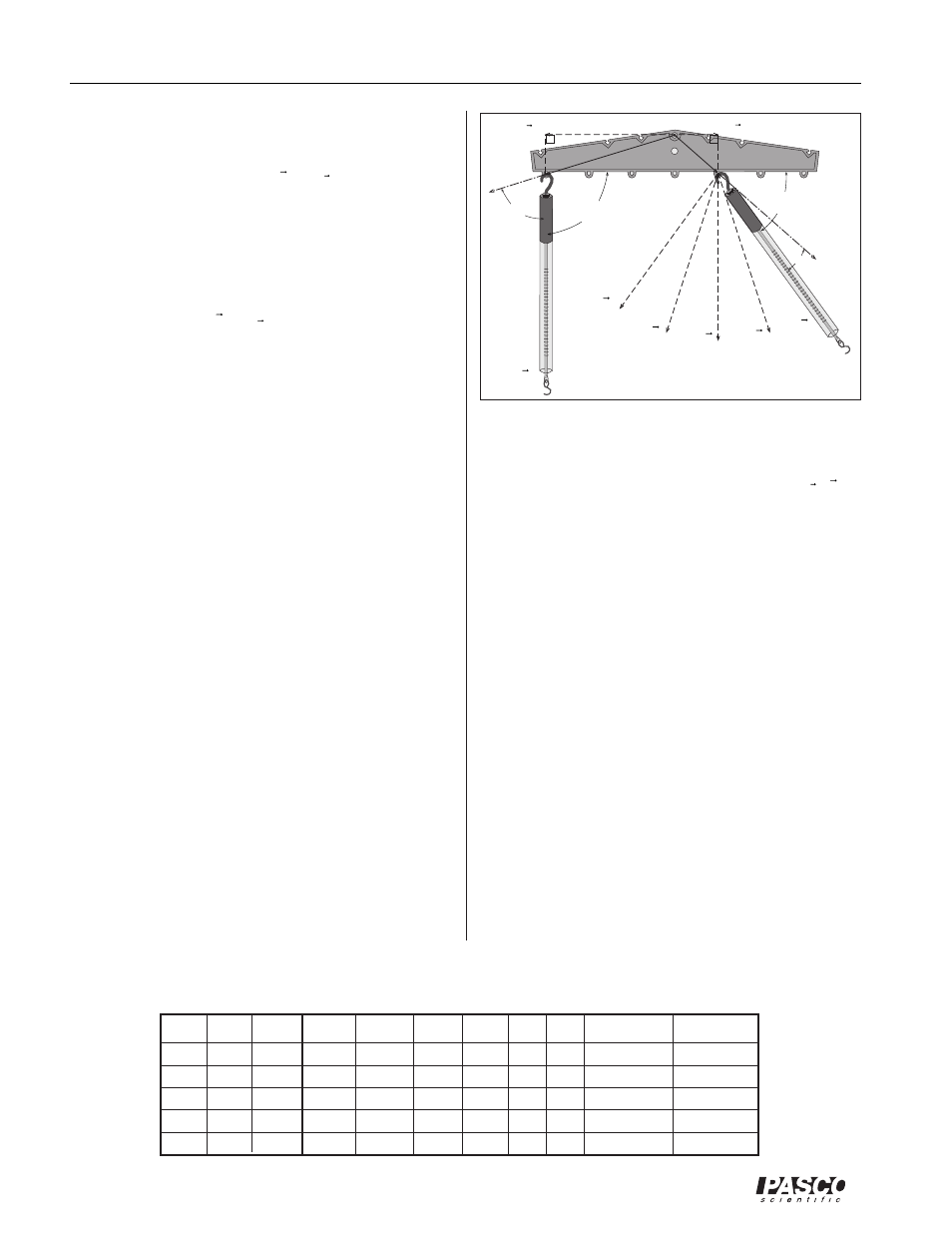
➀
Suppose you were to hold one of the scales at an angle
of 90
o
with respect to the lever arm, r
h
, and pull on it
with a steady force. Meanwhile you can pull on the
other scale at several
angles other than 90 o from its
lever arm, r
app
, as shown below. Would the magnitude
of the balancing force be less than, greater than, or
equal to the force needed at 90
o
? What do you pre-
dict? Explain.
➁ You should determine exactly how the forces com-
pare to that needed at a 90
o
angle. Determine this
force for at least four different angles and figure out a
mathematical relationship between F, r, and
θ
. Set up
a spreadsheet to do the calculations shown in Table2
below . Hint: Should you multiply the product of the
measured values of r and F by sin
θ
or by cos
θ
to get
a torque that is equal in magnitude to the holding
torque?
Fig 5: Torque at an angle
r
h
(m) F
h
(N)
τ
h
(Nm) r
app
(m) F
app
(N)
θ
(deg)
θ
(rad) cos
θ
sin
θ
r
app
F
app
cos
θ
r
app
F
app
sin
θ
Applied
Torque
Holding
Torque
Table 2
Holding torque:
τ
h
r
app
r
h
φ
1
θ
1
θ
2
F
2
F
3
F
4
F
5
F
1
F
h
r
2
r
1
φ
2