PASCO ME-8949 EQUAL ARM BALANCE - Manual (Page 3)

3
012-05921A Equal Arm Balance
®
(b) (a)
➂ Suppose you find that the lead pellet and the silver
coin seem to have the same mass. How could you
create “stuff” that has twice the mass of either of the
original objects?
Using a Mass Balance
One time honored way that people have used to compare
the mass of two objects is to put them on a balance. If
they happen to balance each other we say that the “force
of gravity” or the force of attraction exerted on them by
the earth is the same, so they must have the same mass.
Fig. 4: A common method of determining mass that
assumes two objects have the same mass if they
experience the same gravitational force.
Using a Balance to Measure an Arbitrary
Mass
➀ Explain how you might measure the passive gravita-
tional mass of an object using the balance, sand, and
standard coin.
➁
Use the Equal Arm Balance with some masses of dif-
ferent sizes and shapes to test your ideas.
This experiment has been adapted from Unit 12:
Rotational Motion
The Rotational Analog of Force – What Should It Be?
If linear equilibrium results when the vector sum of the
forces on an object is zero (i.e. there is no change in the
motion of the center of mass of the object), we would like
to demand that the sum of some new set of rotational
quantities on a stationary non-rotating object also be zero.
By making some careful observations you should be able
to figure out how to define a new quantity which is analo-
gous to force when it comes to causing or preventing ro-
tation. For this set of observations you will need:
• 1 Equal Arm Balance
• 1 clamp stand (to hold the Balance)
• 2 spring scales, 5 N
• 1 ruler
P
ASCO
scientific
EQUAL
ARM
BALANCE
MAXIMUM
T O T A L MASS NOT
T O EXCEED ONE KILOGRAM ME-8949
P
ASCO
scientific
EQUAL
ARM
BALANCE
MAXIMUM
T O T A L MASS NOT
T O EXCEED ONE KILOGRAM ME-8949
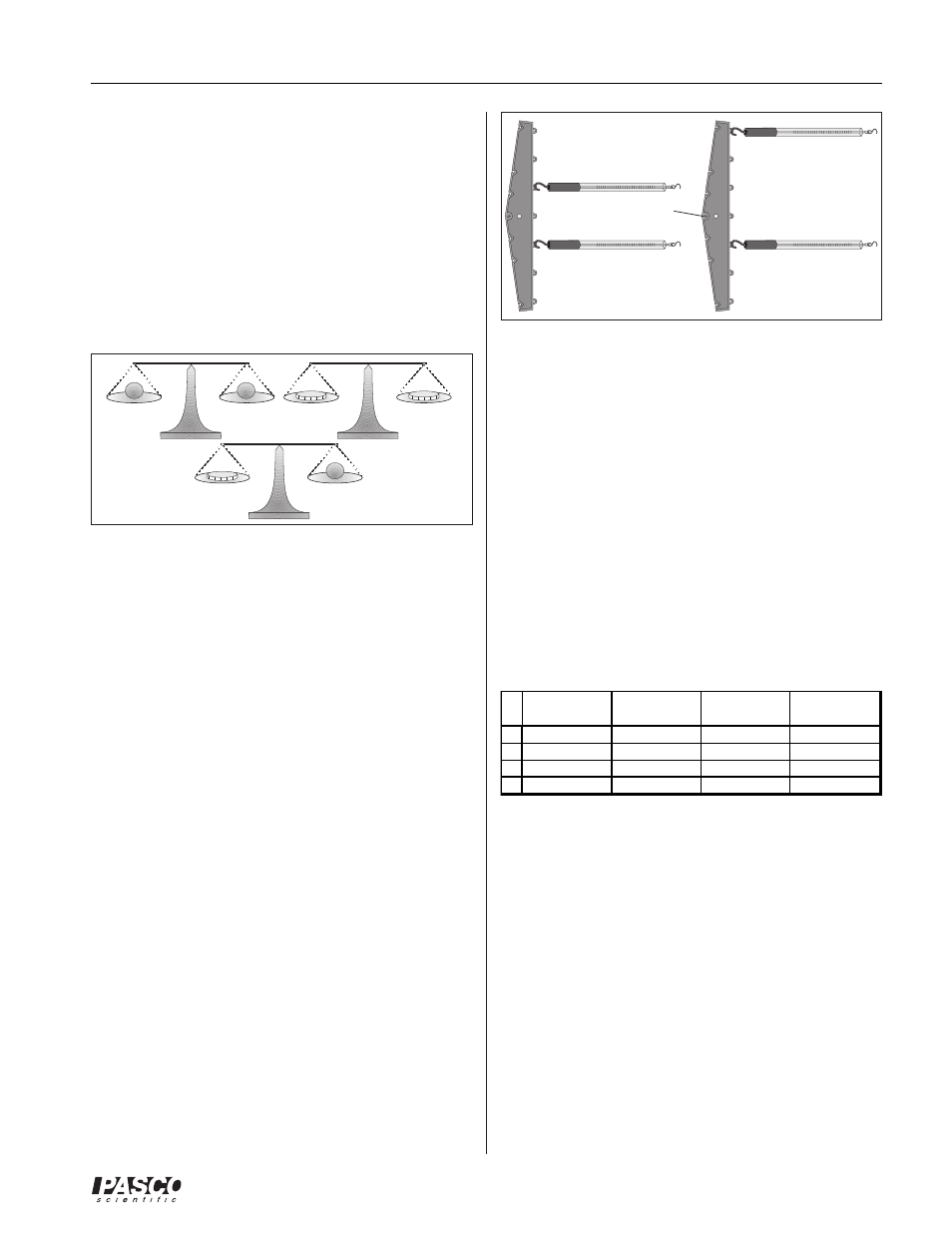
Fig. 5: Equal Arm Balance & Spring Balances
Pivot
Force and Lever Arm Combinations
➀ Rotate the Equal Arm Balance horizontally on the
pivot. Try pulling horizontally with each scale when
they are hooked on loops that are the same distance
from the pivot as shown in Figure 5, diagram (a)
above. What ratio of forces is needed to keep the Bal-
ance from rotating around the pivot?
➁ Try moving one of the spring scales to some other
loop as shown in Figure 5, diagram (b). Now what
ratio of forces is needed to keep the Balance from ro-
tating? How do these ratios relate to the distances?
Try this for several different situations and record
your results in Table 1 below.
➂
What mathematical relationship between the original
force and distance and the balancing force and dis-
tance give a constant for both cases? How would you
define the rotational factor mathematically? Cite evi-
dence for your conclusion.
➃
Show quantitatively that your original and final rota-
tional factors are the same within the limits of experimen-
tal uncertainty for all four of the situations you set up.
The rotational factor that you just discovered is officially
known as torque and is usually denoted by the Greek let-
ter
τ
(“tau” which rhymes with “cow”). The distance
from the pivot to the point of application of a force is de-
fined as the lever arm for that force.
Table 1
Original Original Balancing Balancing
Force (N) Distance (cm) Force (N) Distance (cm)
1
2
3
4