PASCO WA-9857 String Vibrator - Manual (Page 18)

String Vibrator Standing Waves In Strings
18 ®
adjusted to the frequency of the driving vibrator, one vibrational mode will occur at a much
greater amplitude than the other modes.
For any wave with wavelength
λ and frequency f, the speed, v, is
(eq. 1) v =
λ f
The speed of a wave on a string is also given by
(eq. 2)
where F is the tension in the string and
µ is the linear density (mass/length) of the string.
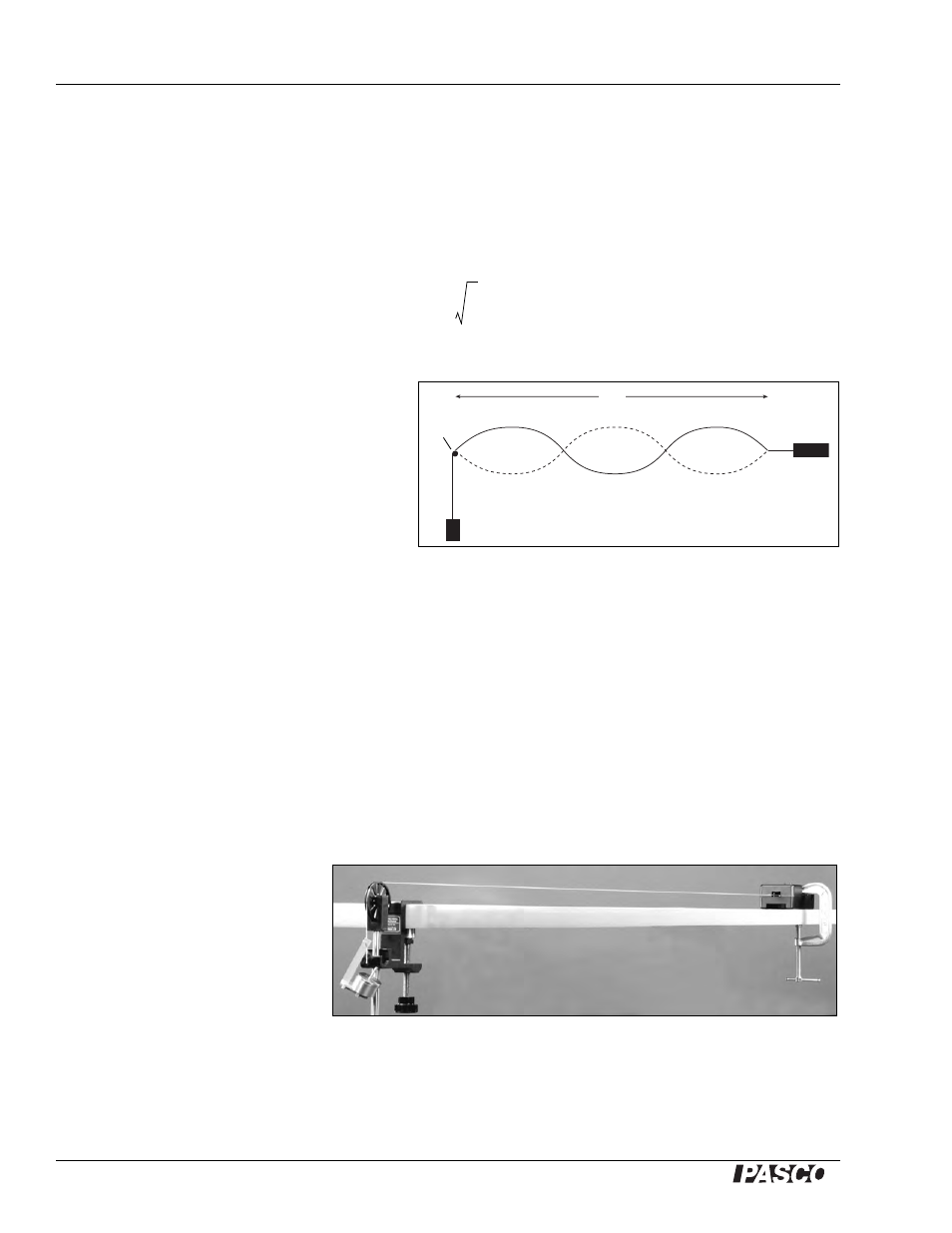
In this experiment, standing waves are set
up in a stretched string by the vibrations of
an electrically-driven String Vibrator. The
arrangement of the apparatus is shown to
the right. The tension in the string equals
the weight of the masses suspended over
the pulley. You can alter the tension by
changing the masses.
L is the length of the string and n is the number of segments. (Note that n is not the number of
nodes). Since a segment is 1/2 wavelength then
(eq. 3)
Setup
1. Measure the exact length of a piece of string several meters long. Measure the mass of the
string and calculate the linear density,
µ (mass/length).
(If your balance is not precise enough to measure that length of string, use a much longer
piece of string to calculate the linear density.)
2. As shown in the picture,
clamp the String Vibrator
and pulley about 100 cm
apart. Attach the string to
the vibrating blade, run it
over the pulley, and hang
about 100 g of mass from
it. Cut off the excess string.
3. Measure from the knot where the string attaches to the String Vibrator to the top of the pulley.
This is distance L. (L is not the total length of the string that you measured in step 1.)
4. Connect the AC power supply to the String Vibrator.
v
F
µ
--- =
L
String
String
Vibrator
Hanging
Mass
Pulley
λ
2L
n
------ = n 1 2 3
… , , ,
=