PASCO TD-8564 THERMAL EFFICIENCY APPARATUS - Manual (Page 7)

012-05443A Thermal Efficiency Apparatus
3
Theory
Q
c
Q
h
T
h
T
c
Cold
Reservoir
Hot
Reservoir
Heat
Engine
W
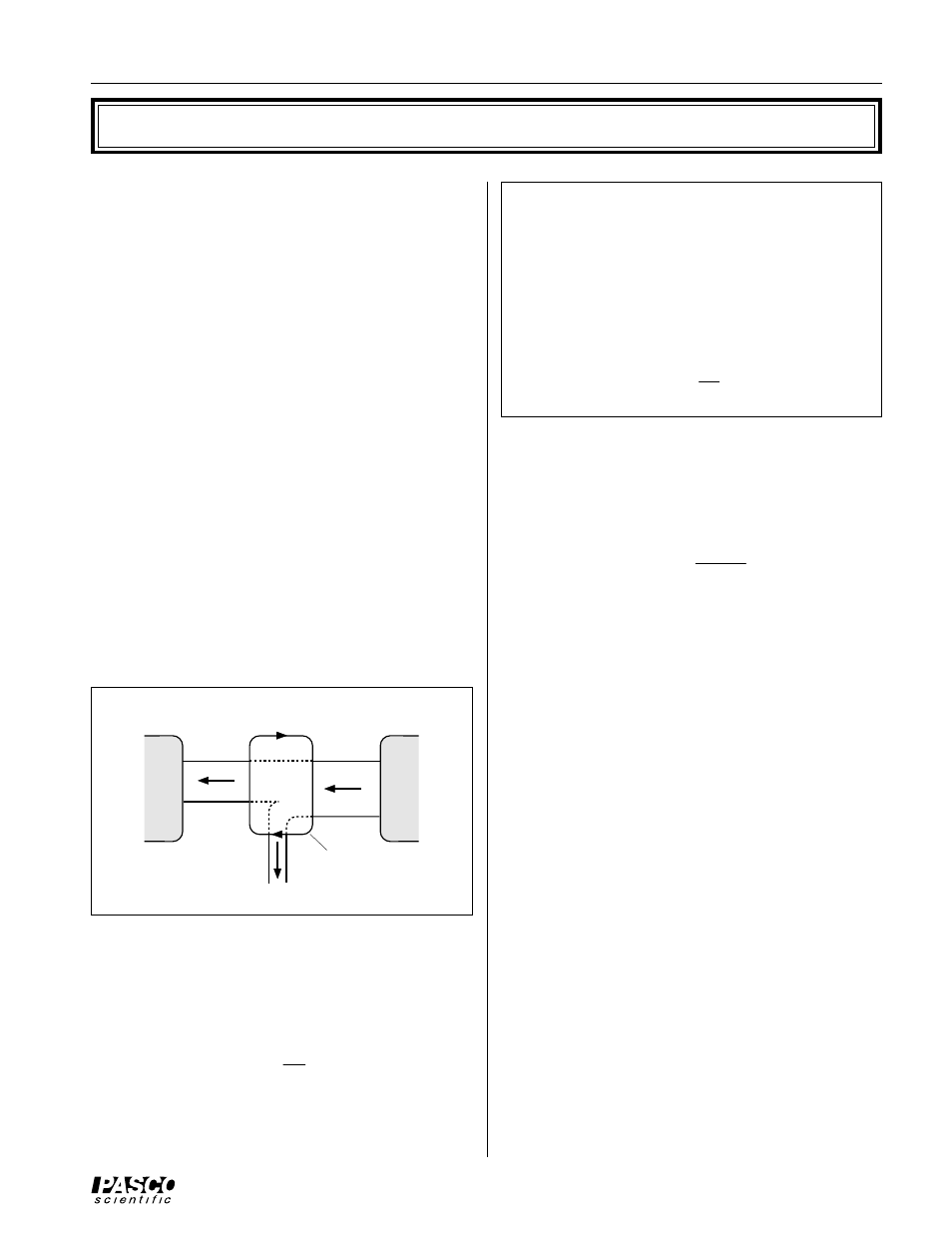
Figure 2: Heat Engine
Heat Engine
Introduction
A heat engine uses the temperature difference between
a hot reservoir and a cold reservoir to do work. Usu-
ally the reservoirs are assumed to be very large in size
so the temperature of the reservoir remains constant
regardless of the amount of heat extracted or delivered
to the reservoir. This is accomplished in the Thermal
Efficiency Apparatus by supplying heat to the hot side
using a heating resistor and by extracting heat from the
cold side using ice water.
In the case of the Thermal Efficiency Apparatus, the
heat engine does work by running a current through a
load resistor. The work is ultimately converted into
heat which is dissipated by the load resistor (Joule
heating).
A heat engine can be represented by a diagram (Figure
2). The law of Conservation of Energy (First Law of
Thermodynamics) leads to the conclusion that
Q
H
= W + Q
C
, the heat input to the engine equals the
work done by the heat engine on its surroundings plus
the heat exhausted to the cold reservoir.
➤ NOTE: Since you will be measuring the rates
at which energy is transferred or used by the
Thermal Efficiency Apparatus all measurements
will be power rather than energy. So
P
H
= dQ
H
/dt and then the equation
Q
H
= W + Q
C
becomes P
H
= P
W
+ P
C
and the
efficiency becomes
e =
P
W
P
H
Carnot Efficiency
Carnot showed that the maximum efficiency of a heat
engine depends only on the temperatures between
which the engine operates, not on the type of engine.
e
Carnot
=
T
H
– T
C
T
H
where the temperatures must be in Kelvin. The only
engines which can be 100% efficient are ones which
operate between T
H
and absolute zero. The Carnot
efficiency is the best a heat engine can do for a given
pair of temperatures, assuming there are no energy
losses due to friction, heat conduction, heat radiation,
and Joule heating of the internal resistance of the
device.
Adjusted Efficiency
Using the Thermal Efficiency Apparatus, you can
account for the energy losses and add them back into
the powers P
W
and P
H
. This shows that, as all losses
are accounted for, the resulting adjusted efficiency
approaches the Carnot efficiency, showing that the
maximum efficiency possible is not 100%.
Actual Efficiency
The efficiency of the heat engine is defined to be the
work done divided by the heat input
e =
W
Q
H
So if all the heat input was converted to useful work,
the engine would have an efficiency of one (100%
efficient). Thus, the efficiency is always less than one.