Step immunity and no r, Sense – Rainbow Electronics MAX5937 User Manual
Page 20
MAX5936/MAX5937
-48V Hot-Swap Controllers with V
IN
Step Immunity and No R
SENSE
20
___________________________________________________
Verification of the Step
Monitor Timing
It is prudent to verify conclusively that all circuit-breaker
and short-circuit faults will be blocked for all ramp
rates. To do this, some form of graphical analysis is
recommended but first, find the value of τ
L,eqv
of the
load by a series of ramp tests as indicated earlier.
These tests include evaluating the load with a series of
V
IN
ramps of increasing ramp rates and monitoring the
rate of V
OUT
rise during the ramp. Each V
IN
ramp
should have a constant slope. The V
OUT
response data
must be taken only during the positive ramp. Data
taken after V
IN
has leveled off at the new higher value
must not be used.
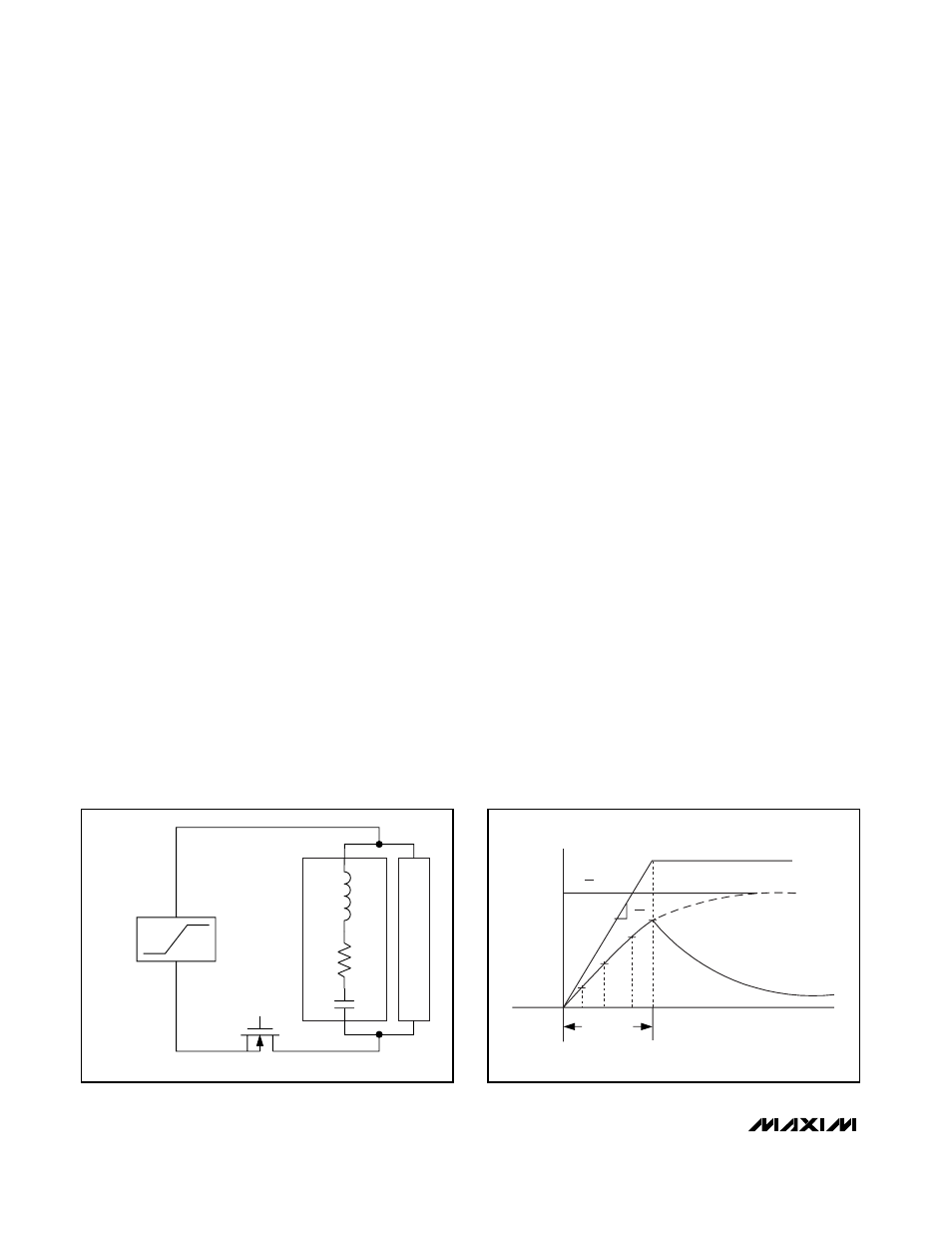
Figure 18 shows the load in parallel with the load
capacitor, C
LOAD
, and the parallel connection in series
with the power MOSFET, which is fully enhanced with
V
GS
= 10V. The objective is to determine τ
L,eqv
from
the V
OUT
response.
Figure 19 shows the general response of V
OUT
to a V
IN
ramp over time t. Equation 1 gives the response of V
OUT
to a ramp of dV/dt. The product (dV/dt) x τ
C
=
∆V
OUT
(max) or the maximum V
OUT
voltage differential if
the V
IN
ramp were to continue indefinitely. The parame-
ter of interest is ∆V
OUT
due to the ramp dV/dt, thus it is
necessary to subtract the DC shift in V
OUT
due to the
load resistance. For some loads, which are relatively
independent of supply voltage, this may be insignificant.
V
OUT
(t) = V
OUT
(t) - R
DS(ON)
x I
LOAD
where I
LOAD
is a function of the V
OUT
level that should
be determined separately with DC tests.
At any time (t) the ∆V
OUT
fraction of ∆V
OUT
(max) is:
∆V
OUT
(t) / [(dV/dt) x τ
C
] = (1-e
(-t / τL,eqv)
)
If V
OUT
(t) is measured at time t, then the equivalent
time constant of the load is found from:
τ
L,eqv
= -t / ln(1 - ∆V
OUT
/ [(dV/dt) x τ
C
])
As mentioned earlier, several measurements of ∆V
OUT
at times t1, t2, t3, and t4 should be made during the
ramp. Each of these may result in slightly different val-
ues of τ
L,eqv
and all values should then be averaged.
In making the measurements, the V
IN
ramp duration
should be such that ∆V
OUT
reaches 2 or 3 times the
selected ∆V
SC
. The ramp tests should include three
ramp rates: ∆V
SC
/ τ
C
, 2 x ∆V
SC
/ τ
C
and 4 x ∆V
SC
/ τ
C
.
The values of τ
L,eqv
may vary over the range of slew
rates due to measurement error, nonlinear dynamics in
the load, and due to the fact that Equation 1 is a simpli-
fication from a higher order dynamic system. The
resulting range of τ
L,eqv
values should be used to vali-
date the performance of the final design.
Having τ
C
, τ
L,eqv
, R
STEP
, and C
STEP
in a graphical
analysis using Equation 1 and Equation 2 can verify the
step monitor function by displaying the relative timing
of t
CB
, t
STEP
, and t
SC
, which are the times when V
CB
,
V
STEP_MON
, and V
SC
voltage thresholds are exceeded.
A simple spreadsheet for this purpose can be supplied
by Maxim upon request. Figures 20, 21, and 22 graphi-
cally verify a particular solution over 3 decades of V
IN
ramp rates. In addition, Figure 22 verifies that this solu-
tion will block all circuit-breaker and short-circuit faults
for even the lowest V
IN
ramp that will cause V
OUT
to
exceed V
CB
.
Figure 18. V
IN
Ramp Test of Load
L
EQU
R
EQV
C
LOAD
LOAD
LOAD CAPACITOR
WITH PARASITICS
V
IN
RAMP
10V
R
DS,ON
Figure 19. General Response of V
OUT
to a V
IN
Ramp
dv
dt
τ
C
dv
dt
V
IN
VOUT.F
VOUTi
V
IN
RAMP
0
t1
t2
t3
t4
