General Tools and Instruments LDM60 - Manual (Page 19)

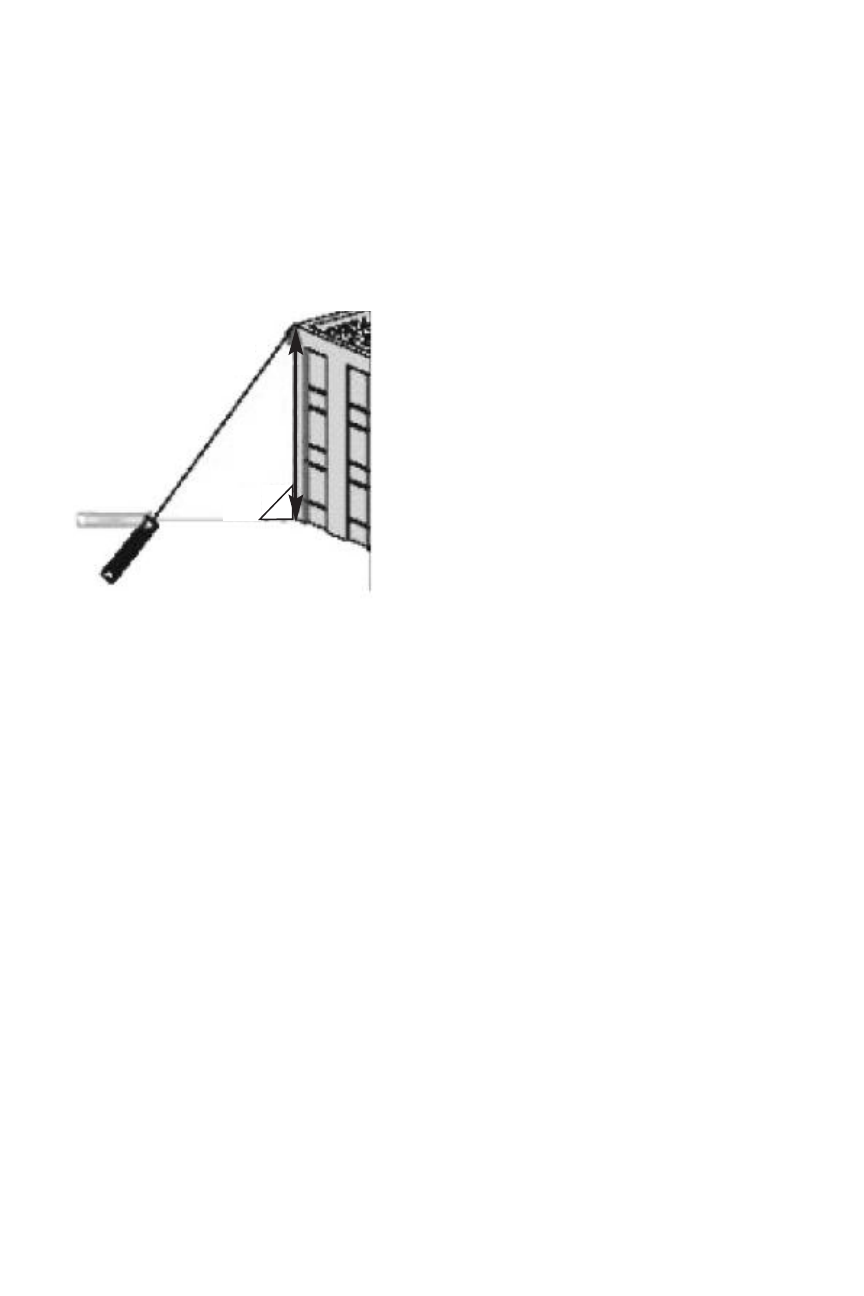
perpendicular to “B”—one of the distances you can measure.
The meter can measure “B” as well as
the distance to the top of the building (“C” in the figure), which
is the hypotenuse of the right triangle. Once the meter has
determined the values of “B” and “C”, it calculates the value
of “A” according to Pythagoras’ famous equation:
A
2 + B 2 = C 2 .
Fig. 8. Triangulating a height
using two inputs
• Triangulation with three inputs. This kind of distance
measurement can be made for distances that do not present
you with a right angle. A good example is measuring the height
of a building from another building across the street through an
open fourth-floor window (Fig. 9). Because the meter and the
bottom of the target building are not both at ground level,
you must measure one common leg “B1/B2” (which is
perpendicular to the wall of the building) and the hypotenuses
of two right triangles “C1” and “C2”. Once these two values
are known, the meter can solve two Pythagorean equations
for the missing values of the other two legs (“A1” and “A2”).
The final calculation, which solves for A—the height of the
building—is A = A1 +A2.
19
C
B
A