NXP Semiconductors UM10301 PCF2123 - Manual (Page 17)

NXP Semiconductors
UM10301
User Manual PCF85x3, PCA8565 and PCF2123, PCA2125
UM10301_1 © NXP B.V. 2008. All rights reserved.
User manual Rev. 01 — 23 December 2008 17 of 52
value is really too high start up problems may occur, but up to 100 k Ω no start up
problems are expected. See 6.1”Oscillation allowance”.
The frequency accuracy of the oscillator depends mainly on the accuracy of the crystal
and on how well the crystal is matched to the oscillator capacitive load (C
L
). A too small
capacitive load results in the oscillator running fast, if the capacitive load is greater than
what the crystal was designed for the oscillator and thus clock runs slow. This initial error
is indicated in Fig 7 as
∆f
off
. The largest influence on accuracy is a result of the
temperature dependence of the crystal.
7.1 Modes which don’t work
To keep time with an adequate accuracy it is necessary to use a quartz crystal and thus
the use of a quartz crystal is always assumed in this application note. A very low power
crystal oscillator as used in an RTC requires a different set of parameters compared to a
universal oscillator accepting crystals, RC- and LC networks or a ceramic resonator. The
oscillator circuit is not designed for operating with RC or LC networks neither for use with
a ceramic resonator. Ceramic resonators have a much shorter start up time than crystals,
about 100 times faster. However, they have lower frequency accuracy (initial tolerance,
temperature variations, drift) and since in an RTC accurate timekeeping is the goal,
ceramic resonators are not a good choice for an RTC. Use a crystal.
7.2 Effect of temperature
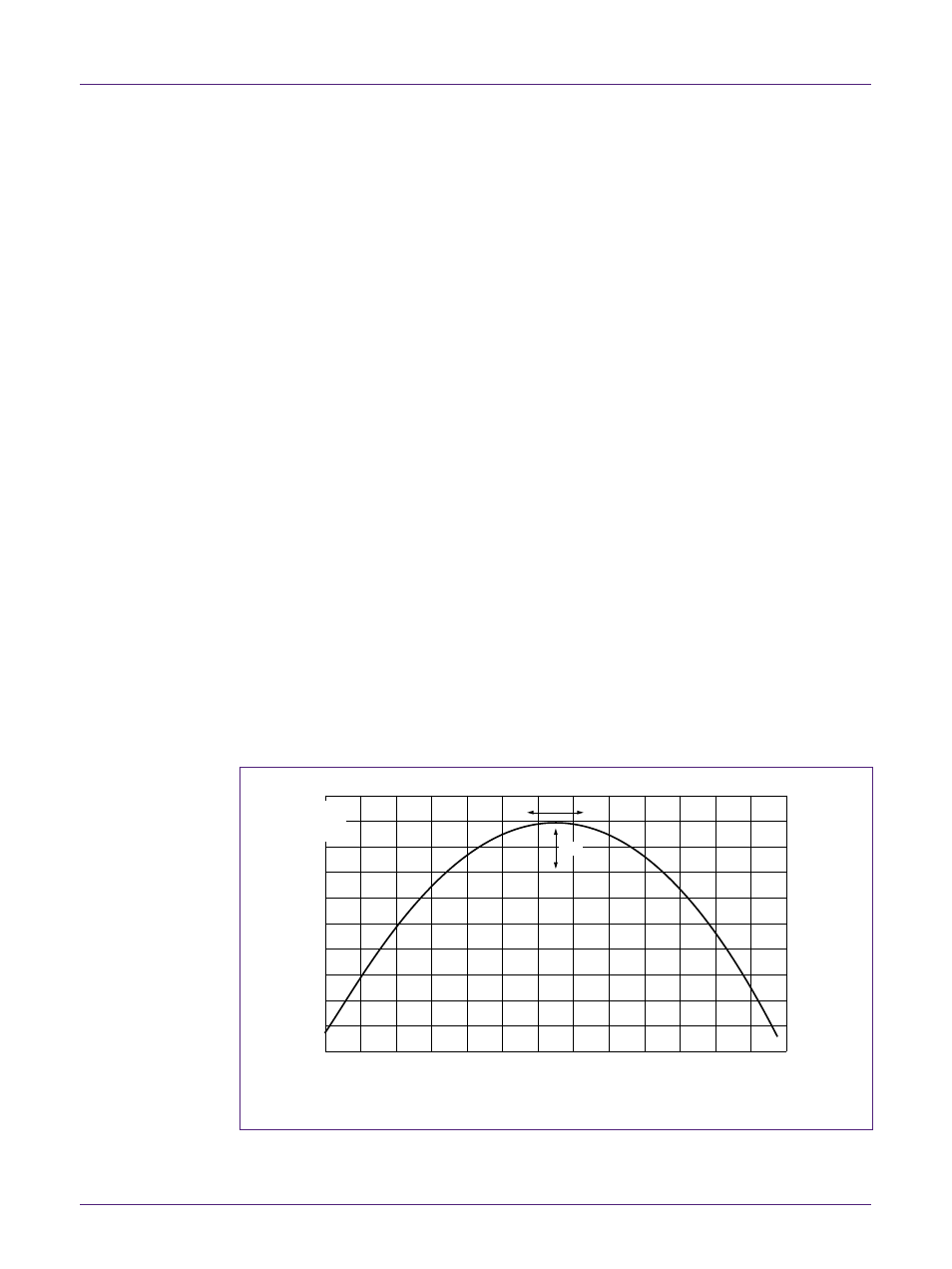
A tuning fork crystal is usually cut such that its frequency over temperature is a parabolic
curve centered around 25 °C, see Fig 7. This means that a tuning fork crystal oscillator
will resonate close to its target frequency at room temperature, but will slow down when
the temperature either increases or decreases from room temperature.
T ( ° C)
− 40 90 80 70 50 30 10 − 10 − 30 60 0 − 20 20 40
001aag901
32.768
kHz
Δ T 0
Δ f
off
− 100
− 60
− 140
− 20
20
− 180
frequency
deviation Δ f/f 0
(ppm)
Fig 7. The deviation in frequency vs. temperature of a typical 32.768 kHz crystal