ElmoMC Multi-Axis Motion Controller-Maestro Motion Control - Manual (Page 52)

Motion Library Tutorial Switch Radius Calculation
MAN-MLT (Ver 2.0)
2-31
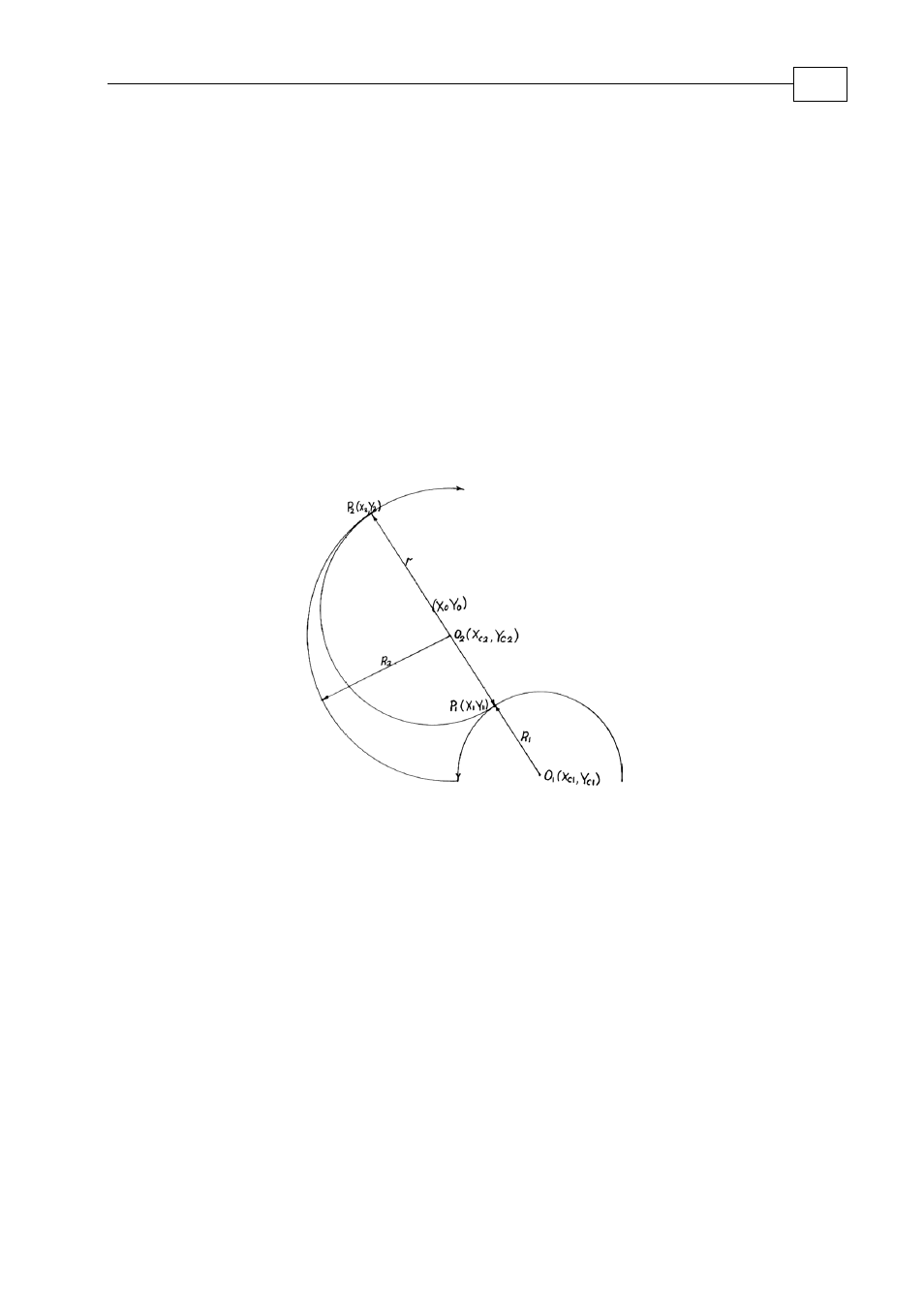
2.3.1 One of two circle arcs intersects the internal area of
the second
If the circle arc C
1
comes from inside of the circle
C
2
– Figure 2-28 (or circle
C
2
continues
inside the circle C
1
), then the switch arc radius must satisfy the necessary condition
r ≤ (R
2
+ h)/2
(2.3.1-1)
where
h
=
ρ(O
2
,P
1
) – distance from the circle C
2
center O
2
to the intersection point
P
1
(X
1
,Y
1
) of the line O
1
O
2
connecting the centers of two circles with the circle arc
C
1
(Figure 2-28). Condition (2.3.1-1) is not always sufficient– only in cases that the points of
intersection
O
1
O
2
with
C
1
and
C
2
belong to
C
1
and
C
2
: P
1
(X
1
,Y
1
)
∈
C
1
and
P
2
(X
2
.Y
2
)
∈
C
2
(Figure 2-28)
.
Figure 2-28
In Figure 2-29 the case when a point of intersection of the line
O
1
O
2
does not belong to
the circle arc
C
1
is presented. Line
O
1
P
1
goes through the circle
C
1
center
O
1
and its
init point
P
1
(X
1
,Y
1
). P
2
(X
2
,Y
2
) –
intersection point of the line
O
1
P
1
with the circle
arc
C
2
(calculation of the circle – line intersection point coordinates can be found in
Appendix 4). By knowing the coordinates of two points
P
1
and
P
2
,
calculate the
distance
d = ρ(P
1
,P
2
).
To define the maximum switch arc radius
r
, use the following system of equations:
(X
o
– X
1
)/(X
2
– X
1
) = r/d
(2.3.1-2)
(Y
o
– Y
1
)/(Y
2
– Y
1
) = r/d
(2.3.1-3)