1 line continues outside the circle (figure 2-17), K – q), Q(x – x – ElmoMC Multi-Axis Motion Controller-Maestro Motion Control User Manual
Page 41: R = [2rρ
Motion Library Tutorial
Switch Radius Calculation
MAN-MLT (Ver 2.0)
2-20
By (a1.6) we have
X
p
= (Y
o
– Y
1
+ kX
1
– qX
o
)/(k – q) = (–
80000
+
56569
–
56569 - 0
)/(1+1) = –
40000
Yp =
Y
o
+ q(X – X
o
) = -80000 – (–40000 - 0) = –40000.
Distance
ρ
1
= ρ(P
3
,P
2
)
= [(–40000 + 56569)
2
+ (–40000 + 56569)
2
]
1/2
=
23432
For the maximum switch radius we get from (3.1.3-5)
r = [2Rρ
1
– (ρ
1
)
2
]/(2R) =
[2*80000*23432 - 23432
2
]/160000 = 20000
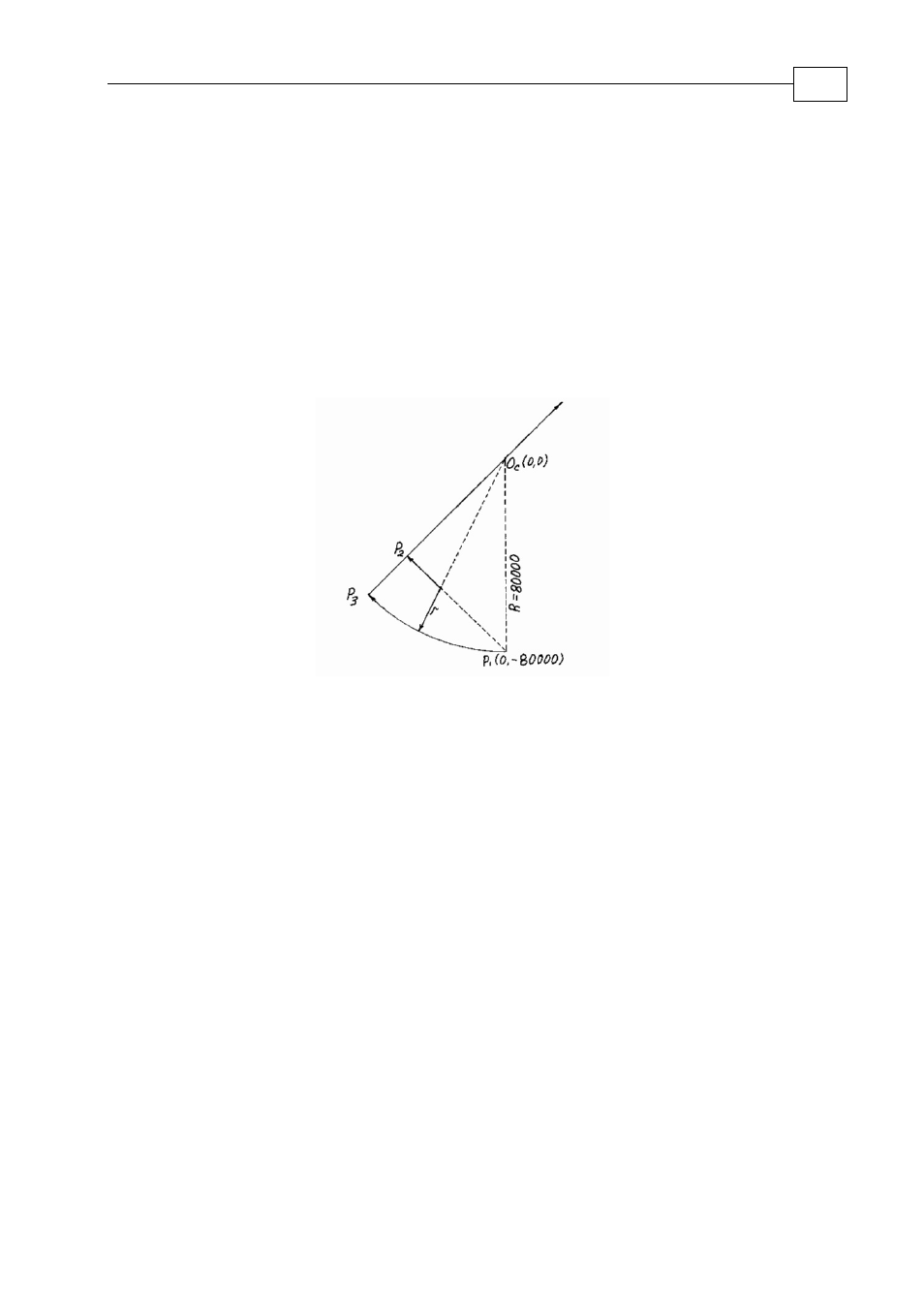
Figure
2-16
2.2.2 Switch arc radius calculation by the distance from the
intersection point
If svc = 3 mode (vsd = d is given) is considered and it is important to know the switch arc
radius r to check if end velocity and vector acceleration satisfy (1-1). If d – distance from the
point (X
i
,Y
i
) to the point (X
first
,Y
first
) is given, then it can be useful to re-calculate r as a
function of parameters d and R (we have to know r to check condition 1-1).
Consider three possible cases of a circle and switch arc positions relative to the line.
2.2.2.1 Initial circle center and switch arc center belong to the
same half-plane
2.2.2.1.1 Line continues outside the circle (Figure 2-17)
As in case of the switch arc center coordinates calculation we drop a perpendicular from the
circle center
(X
c
,Y
c
)
on the line and get a projection point
(X
p
,Y
p
).
The length of the
perpendicular
ρ
1
can be defined as
ρ
1
=
[(X
p
– X
c
)
2
+ (Y
p
– Y
c
)
2
]
1/2
(2.2.2.1.1-1)
Define point
(X
1
,Y
1
)
so that
