Psion Teklogix Vehicle-Mount Computer 8590 - Manual (Page 175)

8580/8590 Vehicle-Mount Computer User Manual D-5
Appendix D: Mechanical Dynamic Loading
Approximate Solution For Elastomer Spring Selection
D.4.1 Approximate Solution For Elastomer Spring Selection
This model applies to the oscillatory mass at the device's center of gravity. This lies
around 120 mm above the mounting surface of the group of springs and also
displaced from it. To determine the spring constant for an individual elastomer
spring, the leverages and arrangement of the springs (here in a triangle) must also be
considered.
Furthermore, each of the 4 elastomer springs connected in parallel must deliver one
third of the total spring constant, i.e., 78 N/mm / 3 = 26 N/mm.
To simplify matters, of the 6 possible degrees of freedom we will only consider
those with the greatest deflection in the case of the 8580. In other words: We
observe the display as it oscillates towards or away from us (a combination of
rotational and longitudinal oscillation).
Comparative measurements for precisely the arrangement displayed in Table-top
attachment with elastomer springs diagram on the previous page:
Attachment (construction of the mounting bracket, quantity and position of the
elastomer springs) show that the individual spring must be stiffer by a factor of 25
for the mathematical model stated above to be applied.
Important: Factors for other mountings with elastomer springs must be cal-
culated through testing!
As a result, this model gives a value of 26 N/mm x 22.5 = 585 N/mm for the
required single spring constant.
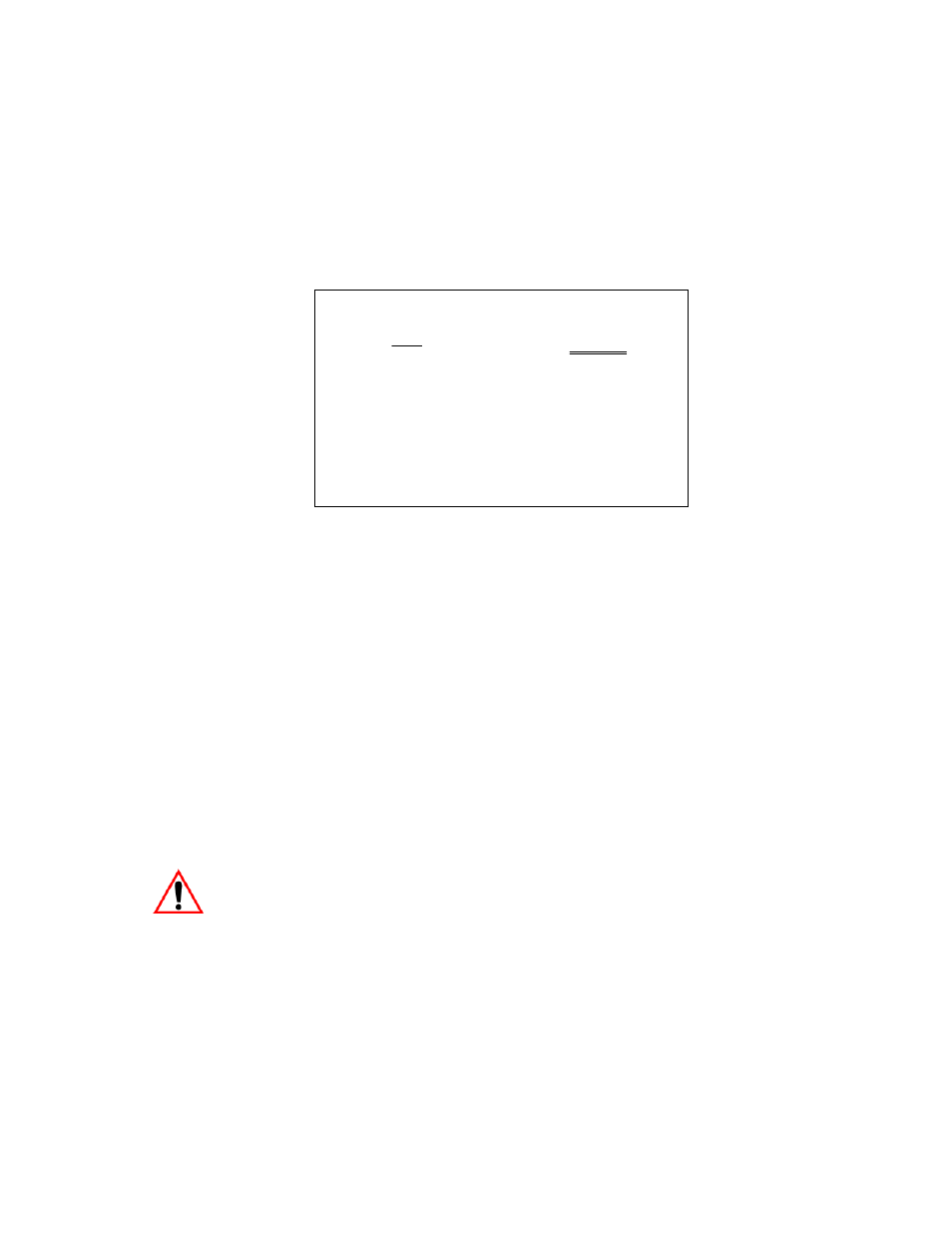
Since ω² = c / m, we obtain the following relationship:
Where:
m = oscillatory mass = 5 kg
f
e
= natural frequency = 20 Hz
c = spring constant in N/mm
mm N f m f m c
e e
/ 78 039 , 0
1000
² 4
2 2 = ⋅ ⋅ ≈ ⋅ ⋅ ≅
π