A circle that passes through 3 points – Sharp EL-5230 User Manual
Page 97
95
Chapter 8: Application Examples
P (X
1
, Y
1
)
S (X
3
, Y
3
)
Q (X
2
, Y
2
)
O (X, Y)
X
1
–X
Y
1
–Y
R
R
R
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(Y
2
–Y
3
) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(Y
1
–Y
2
)
2{(X
1
–X
2
)(Y
2
–Y
3
) – (X
2
–X
3
)(Y
1
–Y
2
)}
X =
------ 1
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(X
2
–X
3
) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(X
1
–X
2
)
2{(Y
1
–Y
2
)(X
2
–X
3
) – (Y
2
–Y
3
)(X
1
–X
2
)}
Y =
------ 2
R =
(X – X
1
)
2
+ (Y – Y
1
)
2
------ 3
GM – HK
2 (IM – JK)
X =
GJ – HI
2 (KJ – MI)
Y =
* Calculate intermediate
values.
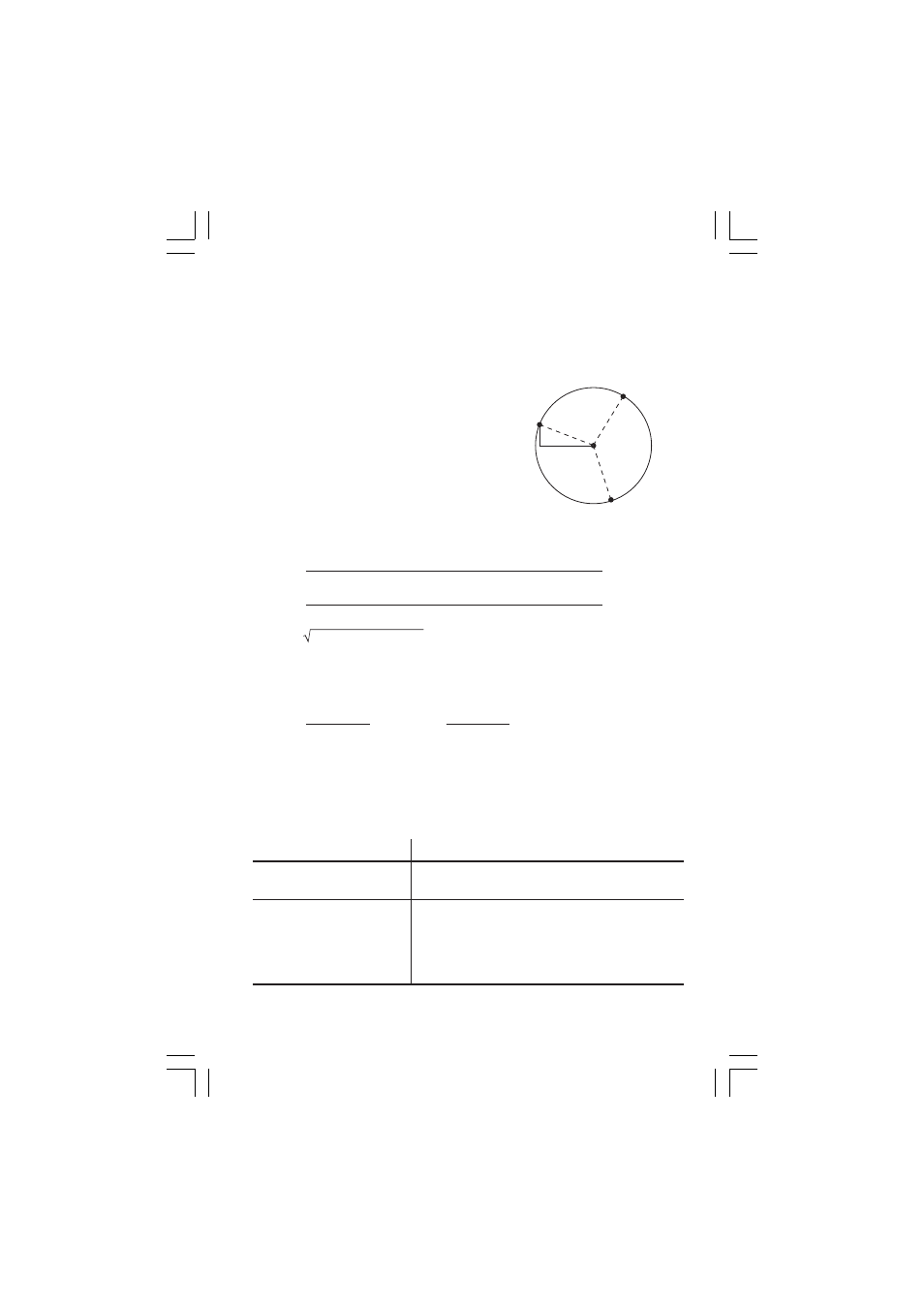
A circle that passes through 3 points
When three different points, P (X
1
, Y
1
), Q (X
2
, Y
2
), S (X
3
, Y
3
) are given,
obtain the center coordinates O (X, Y) and the radius R of the circle that
passes through these points.
To satisfy the above conditions, the
distances between P, Q, S and O
should be equal. as they are the
radius of the same circle. Therefore,
PO = QO = SO = R
Using the Pythagorean theorem,
PO
2
= (X
1
– X)
2
+ (Y
1
– Y)
2
= R
2
QO
2
= (X
2
– X)
2
+ (Y
2
– Y)
2
= R
2
SO
2
= (X
3
– X)
2
+ (Y
3
– Y)
2
= R
2
then
To enhance both readability and writability of the program, intermediate
variables G, H, I, J, K and M are used.
The above equations reduce to
1.
Press b 2 1 0 to open a window for creating a NEW program.
2.
Type CIRCLE for the title then press e.
• A NEW program called ‘CIRCLE’ will be created.
3.
Enter the program as follows.
Program code
Key operations
Print”ENTER COORDS
i 1 @ a ENTER s COORDS
; e
G=X≥Œ+Y≥Œ-X√Œ-Y√Œ
; G ; = @ v X1 e
e A + @ v d Y1 e
e A - @ v d d X2
e e A - @ v d
d d Y2 e e A e
