Casio fx-9750G Implicit Function Graphs - Manual (Page 5)

227
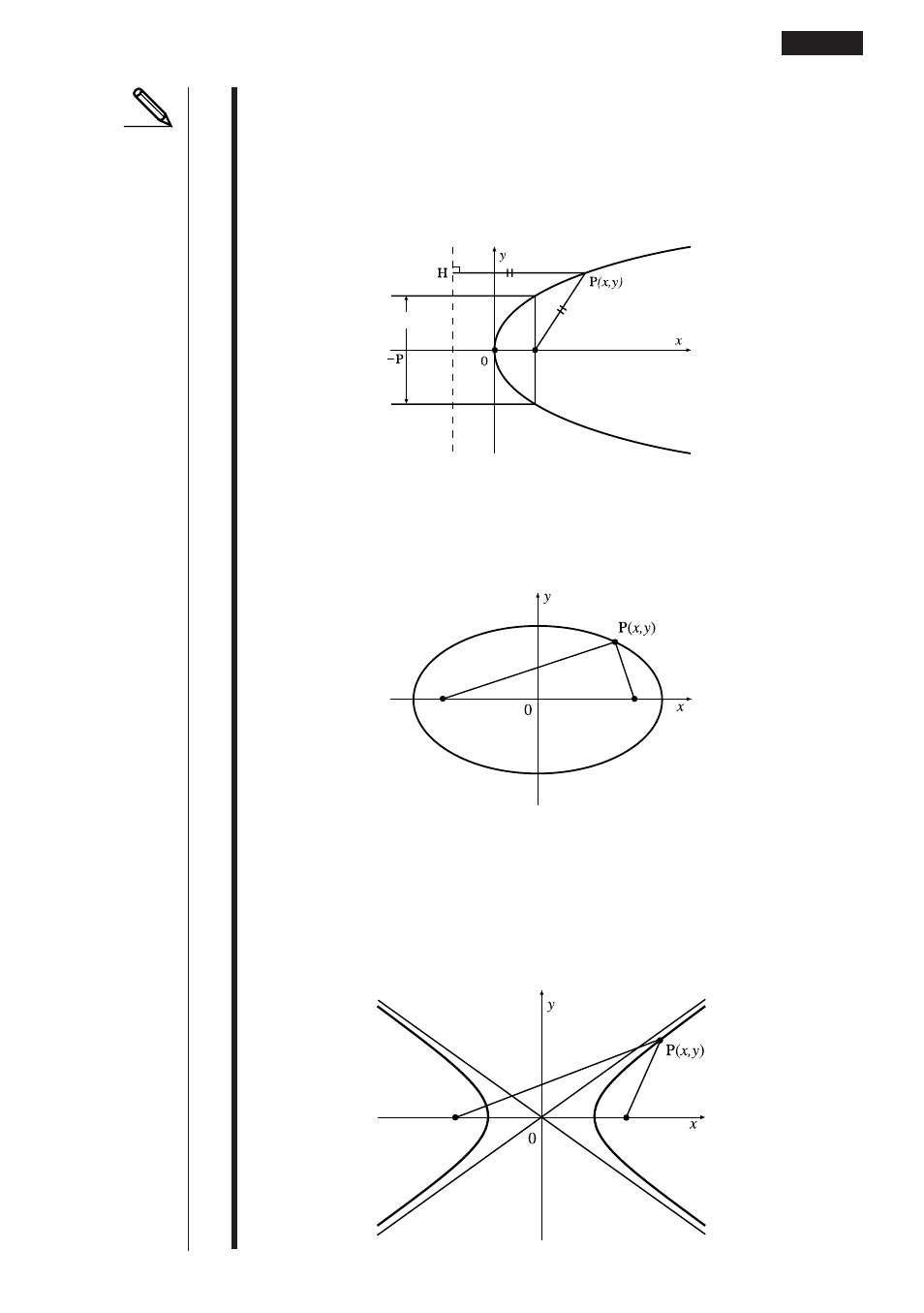
• A parabola is the locus of points equidistant from fixed line l and fixed point F
not on the line. Fixed point F is the “focus,” fixed line l is the “directrix,” the
horizontal line that passes through the focus directrix is the “axis of symmetry,”
the length of a straight line that intersects the parabola, passes through the
locus, and is parallel to fixed line
l is the “latus rectum,” and point A where the
parabola intersects the axis of symmetry is the “vertex.”
• An ellipse is the locus of points the sum of the distances of each of which from
two fixed points F and F’ is constant. Points F and F’ are the “foci,” points A, A’,
B, and B’ where the ellipse intersects the
x - and y -axes are the “vertexes,” the
x -coordinate values of vertexes A and A’ are called x -intercepts, and the y -
coordinate values of vertexes B and B’ are called y -intercepts.
• A hyperbola is the locus of points related to two given points F and F’ such that
the difference in distances of each point from the two given points is constant.
Points F and F’ are the “foci,” points A and A’ where the hyperbola intersects
the x -axis are the “vertexes,” the x -coordinate values of vertexes A and A’ are
called x -intercepts, the y -coordinate values of vertexes A and A’ are called y -
intercepts, and straight lines i and i ' , which get closer to the hyperbola as they
move away from the foci are “asymptotes.”
Axis of symmetry
Latus rectum
Directrix l
Vertex A
Focus F (p, 0)
Graphing an Implicit Function
14 - 2
x -intercept A’
Focus F’ Focus F
x -intercept A
y -intercept B’
y -intercept B
Focus F' Focus F
Vertex
A’ Vertex
A
Asymptote l
Asymptote l'