F 1 2, A j p, P 1 t = 3 – Casio fx-570MS User Manual
Page 34: Example 1
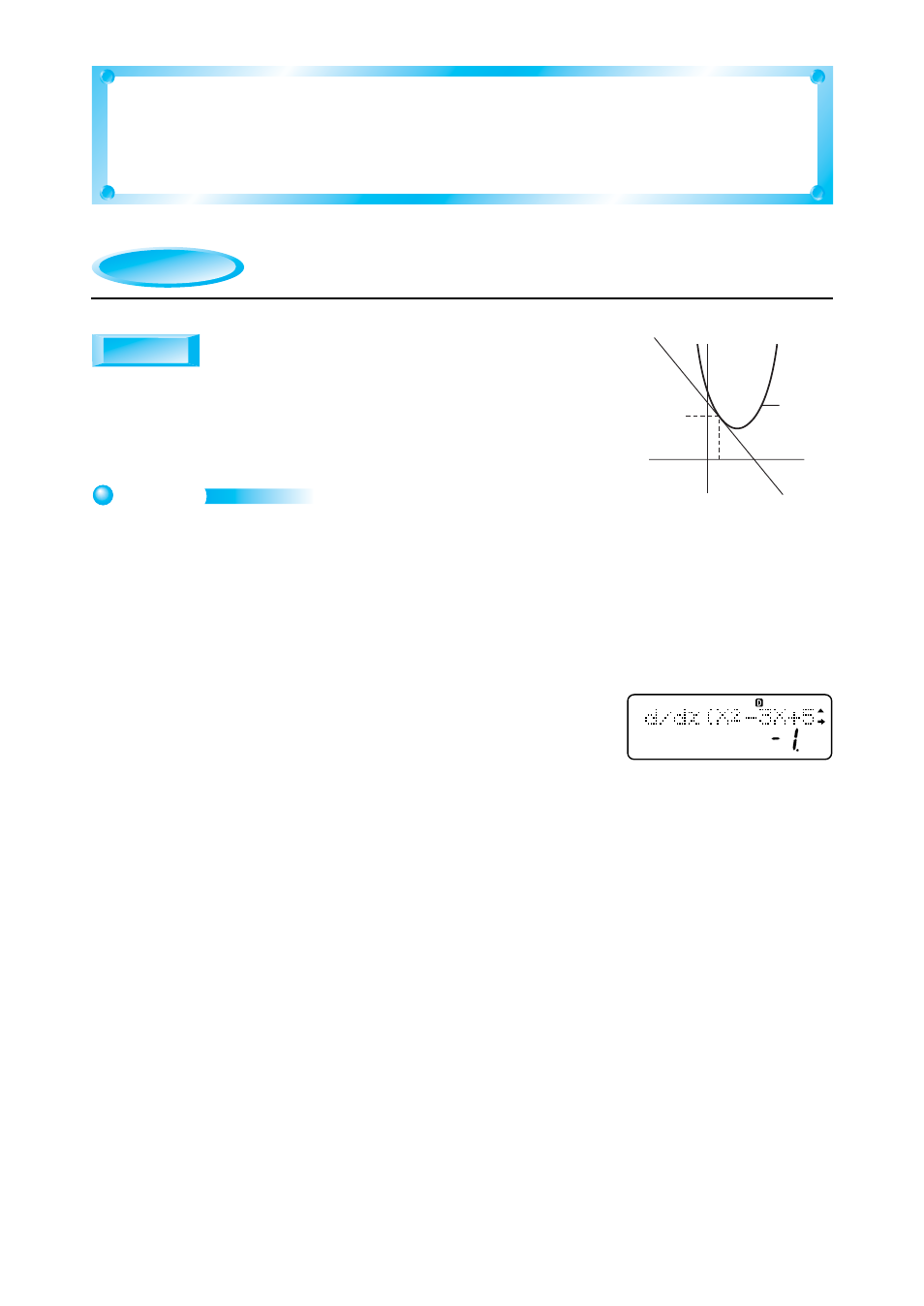
– 31 –
Solving Differentials, with an
Emphasis on the Derivative
(fx-100MS/fx-115MS/fx-570MS/fx-991MS only)
Example 1
Example 1
Explanation
Explanation
Operation
Determine the equation for a tangent line at (1, 3) on
y
=
x
2
– 3
x
+ 5.
Derivative
f
' (
a
) at
x
=
a
on
y
=
f
(
x
) is the slope of the tangent line at
x
=
a
. Also, the tangent line passes through (
a
,
f
(
a
)), which means
that its equation is
y
=
f
' (a) (
x
–
a
) +
f
(
a
).
1
.
Select the COMP Mode.
F 1
2
.
Determine derivative
f
' (1) at
x
= 1 on
y
=
x
2
– 3
x
+ 5.
A J p
x K ,
3
p x +
5
P 1 T =
3
.
Determine
f
' (1) = –1.
4
.
The form of an equation for a tangent line is
y
= –
x
+
c
, which can be transformed to
c
=
y
+
x
.
Since this tangent line passes through (1, 3), substitute these values.
c
=
y
+
x
= 3 + 1
5
.
This produces c = 4.
Based on the above, the equation for the tangent line is
y
= –
x
+ 4.
a
f (x)
f (a)
tangent line
