Ocean Optics Collimation tester - Manual (Page 3)

Collimation Tester Instructions
CT-10000-000-05-201401 3
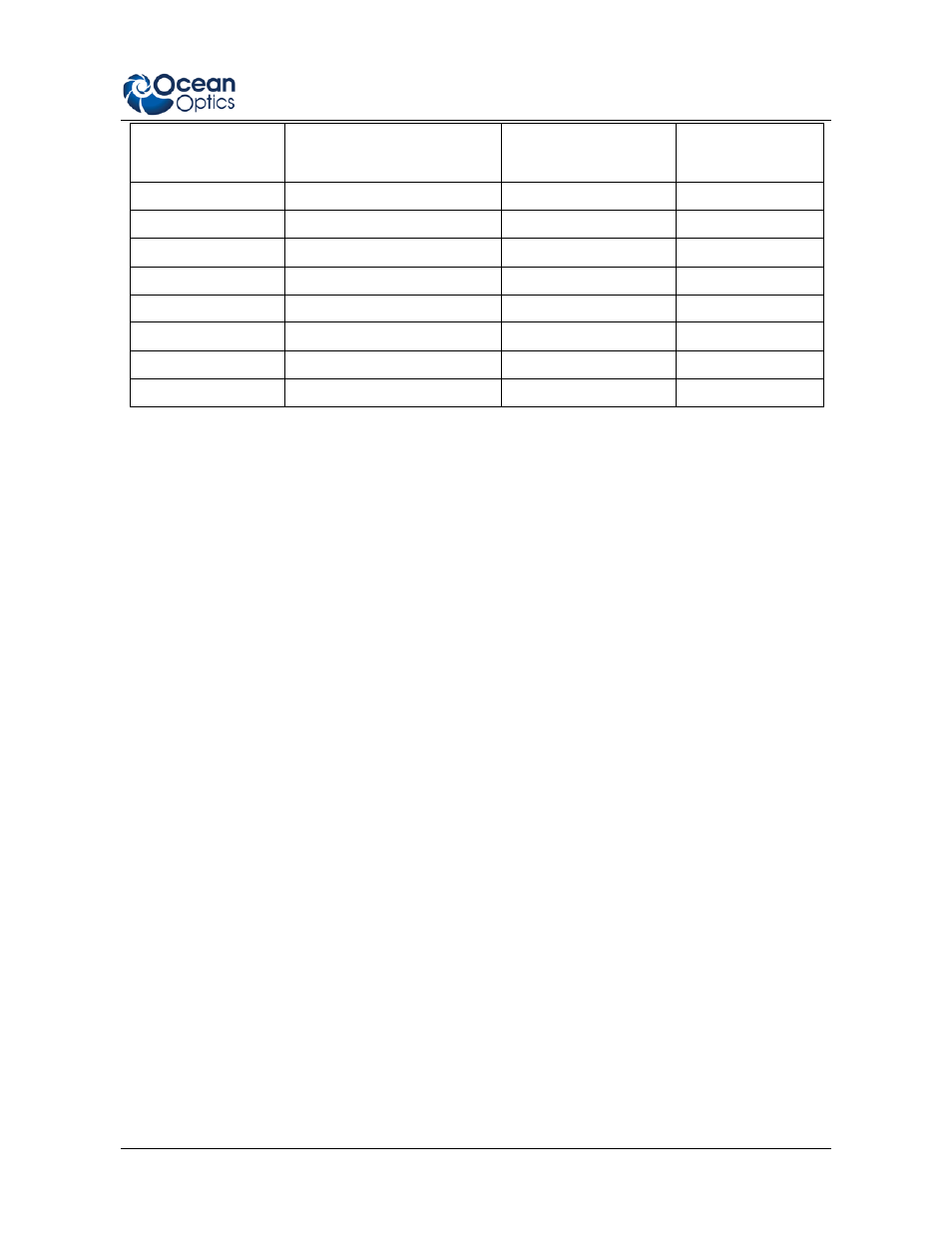
Collimation Tester Aperture Size (in millimeters) Center thickness in
inches +/-.005"
Wedge angle in arc
seconds
CT-10 10 .040 22.5
CT-20 20 .118 11.8
CT-50 50 .375 4.7
CT-75 75 .500 3.2
CT-100 100 .500 2.4
CT-125 125 .625 1.9
CT-150 150 .767 1.6
CT-200 200 1.50 1.2
Using the Collimation Tester for Quantative
Measurements
Ocean Optics’ collimation testers are shearing interferometers. There are many shearing
interferometers but what they have in common is that the wavefront divided in amplitude, some shift
applied to one or both portions, which are then recombined to form an interference pattern. In the
collimation tester, the division arises from reflection at two faces of a slightly wedged plate. The shift
is due to the displacement from the plate thickness and the recombination occurs in the overlapped
images on the screen. Since the wavefront is being compared to itself rather than a reference flat
wavefront, interpretation of the fringes differs from the usual interferometer where the departure from
planarity is indicated by a fringe displacement. In the collimation tester, departure from planarity is
indicated by fringe slope. A treatment of the complete interpretation and analysis of shearing
interferograms is given by Rimmer(1).
Wavefront Curvature
The collimation tester was designed as a null instrument to indicate when the incident beam is parallel.
However, with large radius, spherical wavefronts, the fringes remain linear and can be analyzed to
determine the wavefront curvature (2)(3). With two, separated, spherical wavefronts, the interference
pattern can be treated in the same manner as the 2-pinhole experiment.
In the collimation tester, there are two separations:
• A vertical angle due to the wedge, and
• A horizontal angle proportional to the shear (beam displacement) and inversely proportional to
the wavefront radius.
The figure below illustrates the measurements required,
Where: d = Fringe spacing perpendicular to the fringes
A = Angle of the fringes with respect to the cursor
S = Shear