Rainbow Electronics DS1957 - Manual (Page 23)

DS1957
23 of 25
CRC GENERATION
With the DS1957 there are two different types of CRCs (Cyclic Redundancy Checks). One CRC is an
8-bit type and is stored in the most significant byte of the 64-bit ROM. The bus master can compute a
CRC value from the first 56 bits of the 64-bit ROM and compare it to the value stored within the DS1957
to determine if the ROM data has been received error-free by the bus master. The equivalent polynomial
function of this CRC is: X
8 + X 5 + X 4 + 1. This 8-bit CRC is received in the true (non-inverted) form
when reading the ROM of the DS1957. It is computed at the factory and lasered into the ROM.
The other CRC is a 16-bit type, generated according to the standardized CRC16-polynomial function x 16
+ x 15 + x 2 + 1. This CRC is used for error detection when reading/writing the Intermediate Product
Register (IPR), I/O Buffer and Status Memory for fast verification of data integrity. It is the same type of
CRC as is used with NV RAM based iButtons for error detection within the iButton Extended File
Structure. In contrast to the 8-bit CRC, the 16-bit CRC is always returned or sent in the complemented
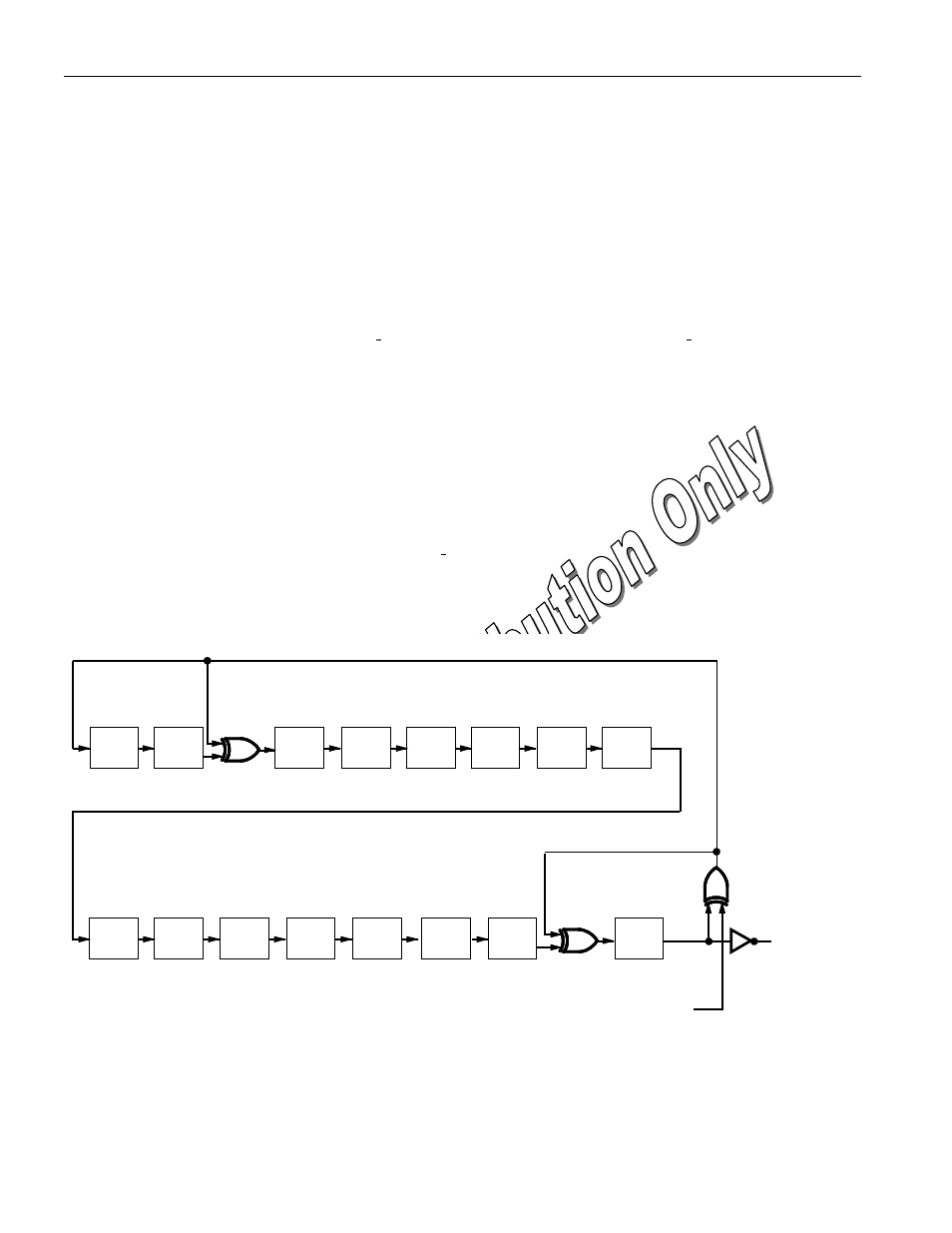
(inverted) form. A CRC generator inside the DS1957 chip (Figure 10) will calculate a new 16-bit CRC as
shown in the command flow chart of Figure 4. The bus master compares the CRC value read from the
device to the one it calculates from the data and decides whether to continue with an operation or to start
all over again.
In every case, the 16-bit CRC value is the result of shifting the command byte into the cleared CRC
generator, followed by the control and/or data bytes as shown in the Data Transfer and Control Function
Flow Chart. For more details on generating CRC values including example implementations in both
hardware and software, see the “Book of DS19xx iButton Standards.”
CRC-16 HARDWARE DESCRIPTION AND POLYNOMIAL Figure 10
1ST
STAGE
2ND
STAGE
3RD
STAGE
4TH
STAGE
5TH
STAGE
6TH
STAGE
7TH
STAGE
8TH
STAGE
X
0
X
1
X
2
X
3
X
4
X
5
X
6
X
7
X
8
Polynomial = X
16
+ X
15
+ X
2
+ 1
9TH
STAGE
10TH
STAGE
11TH
STAGE
12TH
STAGE
13TH
STAGE
14TH
STAGE
15TH
STAGE
16TH
STAGE
X
9
X
10
X
11
X
12
X
13
X
14
X
15
INPUT DATA
X
16
CRC
OUTPUT