Cirrus Logic AN048 - Manual (Page 2)

AN48
2
2. Design Steps
Step 1: Determine the required pass band gain,
H
o
. The circuit parameters require that the magni-
tude of H
o
be greater than or equal to one. H
o
is
also negative due to the inverting op-amp configu-
ration.
Step 2: Determine the minimum input impedance.
Step 3: Select the desired filter type, Butterworth,
Bessel, etc. and the corner frequency, F
c
, for the fi-
nal design. The filter response and corner frequen-
cy determine the pass band phase and amplitude
response. The filter type determines the pole-loca-
tions and therefore alpha and beta. Table 1 lists
the normalized pole locations for several filter
types.
Table 1: Normalized Pole Locations
Step 4: Select convenient values for C 5 and C 2 .
Notice in Step 5 that K and H
o
must be selected
such that
is real.
Step 5: Given F
c
, H
o
, C 2 , C 5 , alpha and beta, cal-
culate R 1 , R 2 and R 3 using the following equa-
tions.
FILTER TYPE
α β
Butterworth 0.7071 0.7071
Bessel 1.1030 0.6368
0.01 dB Chebyshev 0.6743 0.7075
0.1 dB Chebyshev 0.6104 0.7106
_
C5
R3 R1
C2
+
R4
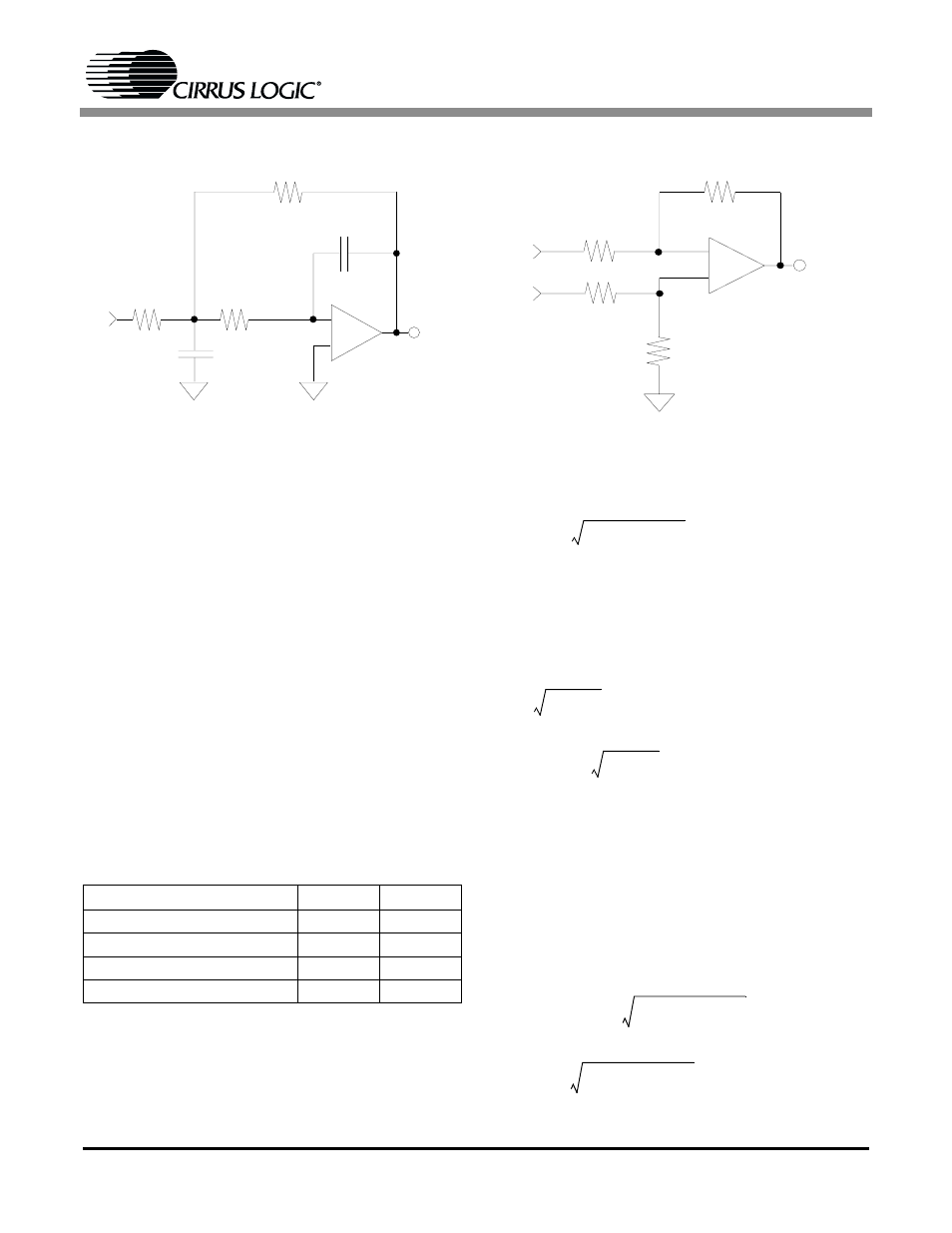
Figure 2. Multiple-Feedback Low-Pass
Filter
_
R1
R1
R4
R4
+
Figure 3. Differential Input Circuit
ζ 2
K 1 H
o
–
( )
–
ζ
α
α 2 β 2
+
---------------------- =
ω
o
2
πF
c
α 2 β 2
+ =
K
C
5
C
2
----- =
R
1
R
4
H
o
–
( )
-------------- =
R
3
1
ω
o
C
2
ζ ζ 2
K 1 H
o
–
( )
–
± [ ]
-------------------------------------------------------------------- =
R
4
ζ ζ 2
K 1 H
o
–
( )
–
±
ω
o
C
5
⋅
------------------------------------------------- =