Rainbow Electronics MAX15058 - Manual (Page 16)

High-Efficiency, 3A, Current-Mode
Synchronous, Step-Down Switching Regulator
MAX15058
16 _____________________________________________________________________________________
As previously mentioned, the power modulator’s dominant
pole is a function of the parallel effects of the load resis-
tance and the current-loop gain’s equivalent impedance:
( )
PMOD
1
S
OUT
LOAD SW
1
f
K 1 D 0.5 1
2 C ESR
R f L
−
=
 
    × − −
   
π Ч Ч + +  
    Ч
 
   
And knowing that the ESR is typically much smaller than
the parallel combination of the load and the current loop:
( )
1
S
LOAD SW
K 1 D 0.5 1
ESR
R f L
−
    × − −
 
  << +
  ×
 
( )
PMOD
1
S
OUT
LOAD SW
1
f
K 1 D 0.5 1
2 C
R f L
−
≈
    × − −
 
π Ч Ч +  
  Ч
 
which can be expressed as:
( )
S
PMOD
OUT LOAD SW OUT
K 1 D 0.5 1
f
2 C R 2 f L C
  × − −
 
≈ +
π Ч Ч π Ч Ч Ч
Note: Depending on the application’s specifics, the
amplitude of the slope compensation ramp could have
a significant impact on the modulator’s dominate pole.
For low duty-cycle applications, it provides additional
damping (phase lag) at/near the crossover frequency
(see the Closing the Loop: Designing the Compensation
Circuitry section). There is no equivalent effect on the
power modulator zero, f
ZMOD .
ZMOD ZESR
OUT
1
f f
2 C ESR
= =
π Ч Ч
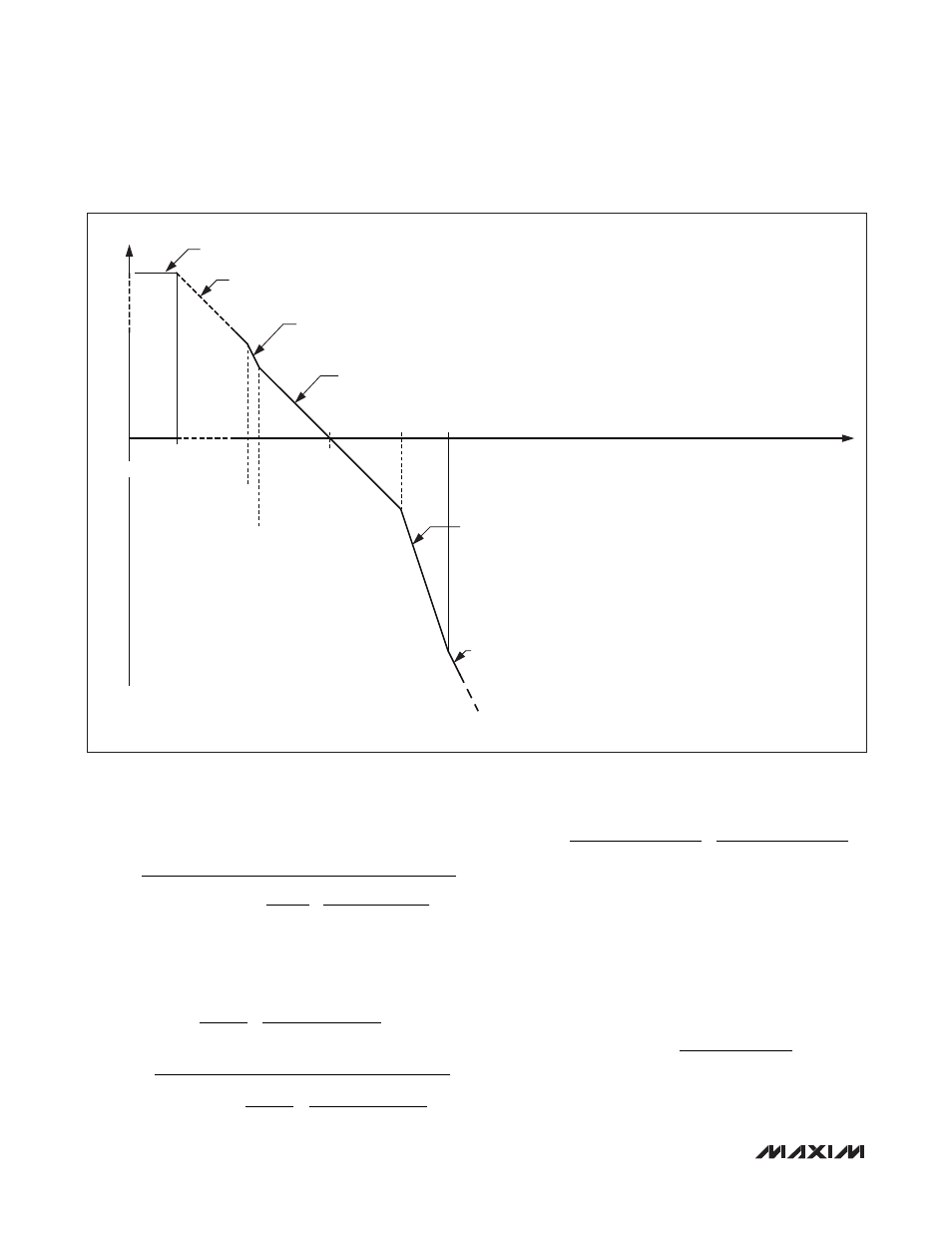
Figure 3. Asymptotic Loop Response of Current-Mode Regulator
GAIN
1ST ASYMPTOTE
R2 × (R1 + R2)
-1 × 10 AVEA(dB)/20 × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1
2ND ASYMPTOTE
R2 × (R1 + R2)
-1 × g MV × (2GC C ) -1 × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1
3RD ASYMPTOTE
R2 × (R1 + R2)
-1 × g MV × (2GC C ) -1 × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ×
(2GC OUT × {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ) -1
4TH ASYMPTOTE
R2 × (R1 + R2)
-1 × g MV × R C × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ×
(2GC OUT × {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ) -1
5TH ASYMPTOTE
R2 × (R1 + R2)
-1 × g MV × R C × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ×
(2GC OUT × {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ) -1 Ч (0.5 Ч f SW ) 2 × (2Gf) -2
6TH ASYMPTOTE
R2 × (R1 + R2)
-1 × g MV × R C × g MC × R LOAD × {1 + R LOAD × [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ×
ESR × {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 Ч (0.5 Ч f SW ) 2 × (2Gf) -2
UNITY
1ST POLE
[2GC C × (10 AVEA(dB)/20 - g MV-1 )] -1
2ND POLE
f PMOD *
3RD POLE (DBL)
0.5 × f SW
2ND ZERO
(2GC OUT ESR) -1
FREQUENCY
f CO
1ST ZERO
(2GC C R C ) -1
NOTE:
R
OUT = 10 AVEA(dB)/20 × g MV-1
f PMOD = [2GC OUT × (ESR + {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 )] -1
WHICH FOR
ESR << {R
LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1
BECOMES
f
PMOD = [2GC OUT × {R LOAD-1 + [K S × (1 - D) - 0.5] × (L × f SW ) -1 } -1 ] -1
f PMOD = (2GC OUT × R LOAD ) -1 + [K S × (1 - D) - 0.5] × (2GC OUT × L × f SW ) -1