Elenco Fiber Optics Voice and Data Kit - Manual (Page 14)

HOW LIGHT TRAVELS THROUGH AN OPTICAL CABLE
SECTION C
-13-
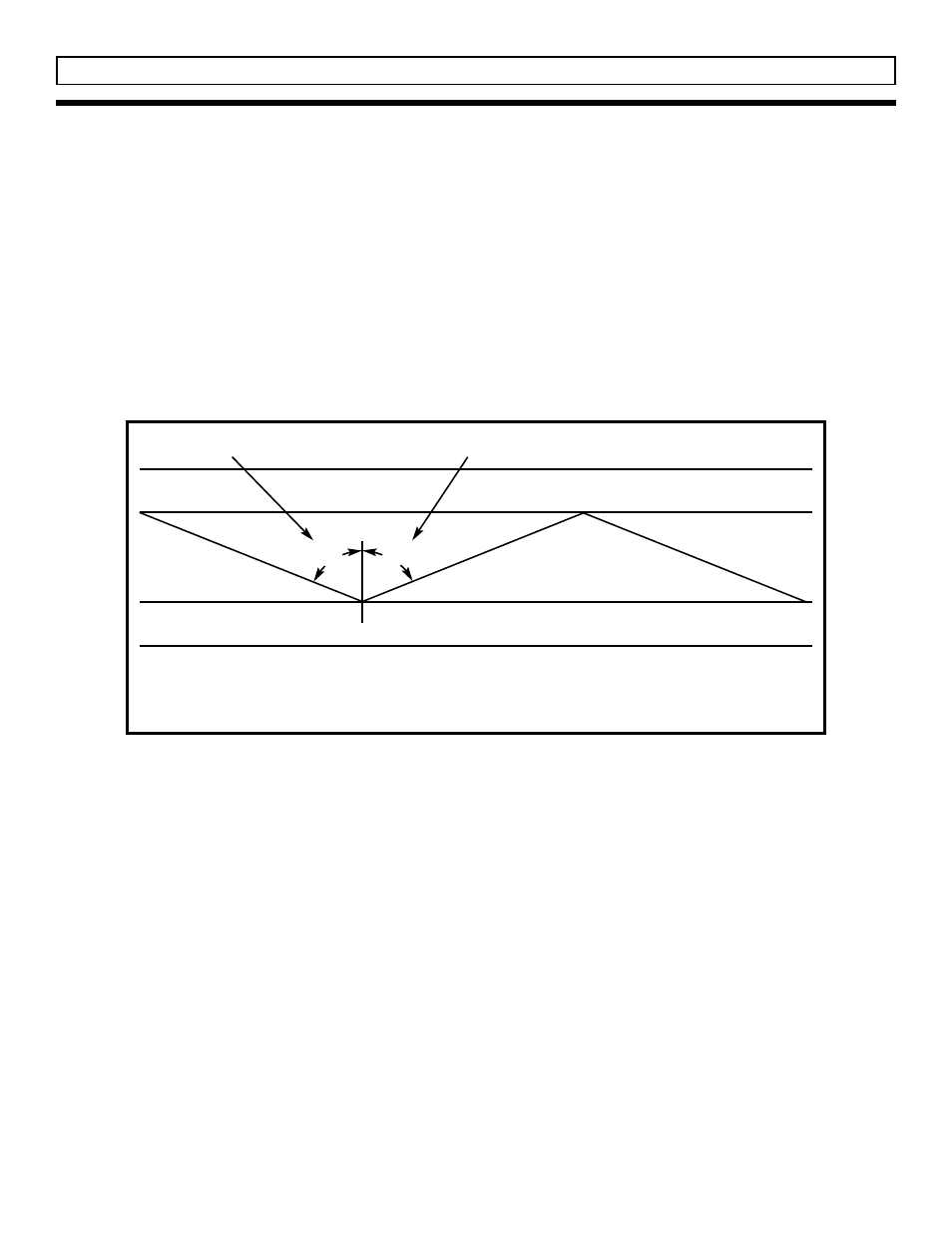
Figure 2F
Light is propagated by
total internal reflection
n
1
n
2
Cladding
Core
Angle of Refraction Angle of Incidence =
81 O 81 O
9 The above paragraphs are reproduced by permission TECHNICIAN’S GUIDE TO FIBER OPTICS 2E (PAGES 40, 44, and 45)
By Donald J Sterling, Jr. - DELMAR PUBLISHERS, INC., Albany, New York, Copyright 1993
To best understand how light propagates through an
optical fiber, let us look at an example. Assume that
the core has a refractive index (n
1
) of 1.48 and the
cladding has a refractive index (n
2
) of 1.46 (these
values are typical for optical fibers). By applying
Snell’s Law, we can calculate the critical angle:
θc = arcsin (n
2
/n
1
)
θc = arcsin (1.46/1.48) = 80.6
O or approximately
81 O
Figure 2F shows that as light rays are injected into
the fiber, they strike the core-to-cladding interface at
an angle greater than that of the critical angle
(80.6
O ). As a result, the light will reflect back to the
core. Since the angles of incidence and reflection
are equal, the reflected light will again be reflected.
The light will continue zig-zagging down the length
of the fiber. Any light that strikes the interface at less
than the critical angle will be absorbed by the
cladding. This total internal reflection forms the
basis of light propagation through a simple optical
fiber.
9