3B Scientific Metal Block Calorimeters - Manual (Page 12)

3B Scientific GmbH ▪ Rudorffweg 8 ▪ 21031 Hamburgo ▪ Alemanha ▪ www.3bscientific.com
Sob reserva de alterações técnicas
© Copyright 2008 3B Scientific GmbH
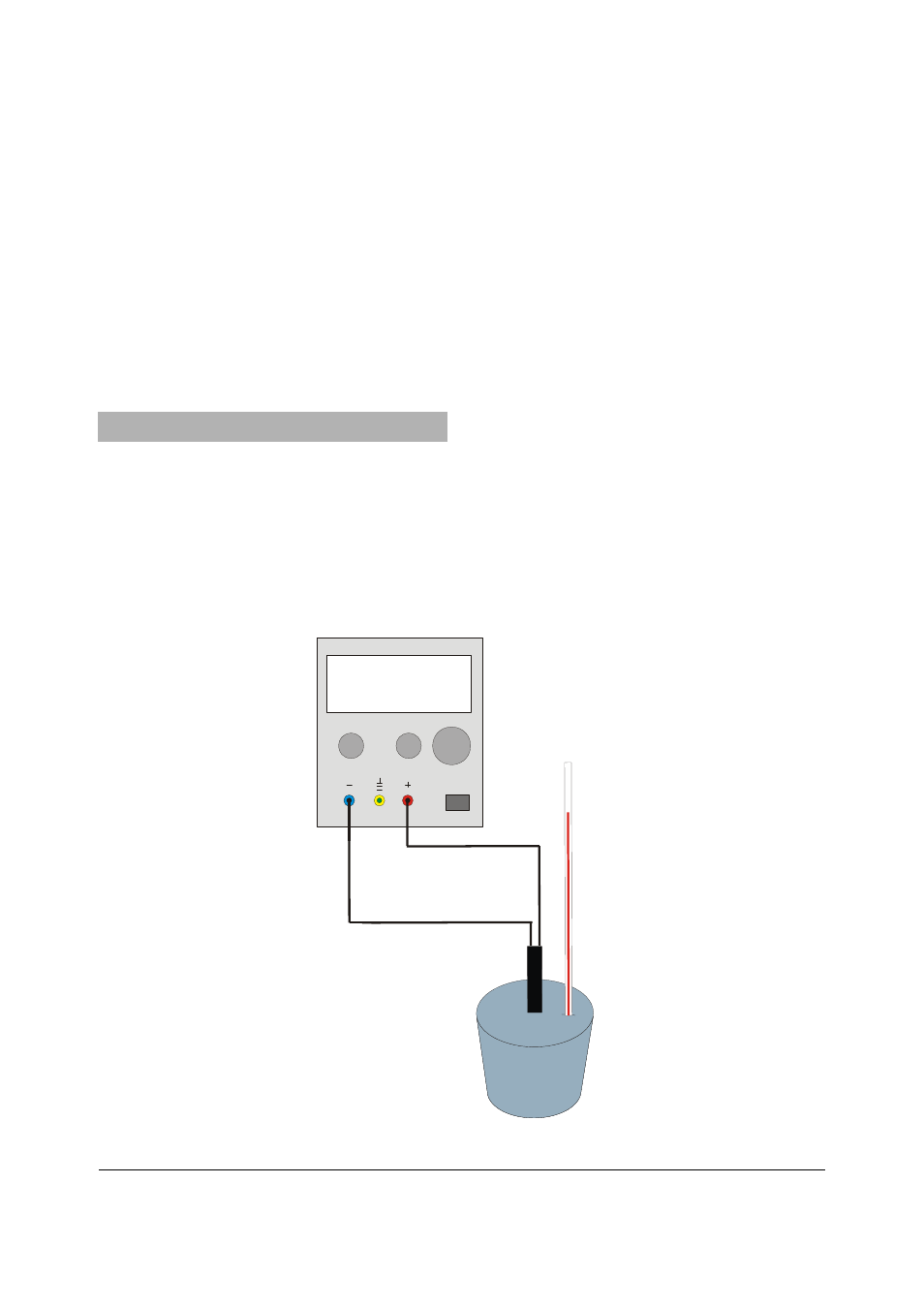
• Esperar alguns minutos antes de começar o curso
das medições. Depois ler a temperatura de inicio
do calorímetro de cilindro.
• Ligar a fonte de alimentação e ao mesmo tempo
começar a medição de tempo.
• Esperar até a temperatura aumentar em aprox.
20° C. Anotar o tempo e a temperatura final.
A capacidade de calor específica é dada por meio da
equação:
( )
1 2
θ − θ ⋅ ⋅ = ⋅ ⋅
c m t U I
com I: Corrente, U: Tensão, t: Tempo, m: Massa do
calorímetro de cilindro c: Capacidade de calor
específica,
θ
1
: Temperatura inicial,
θ
2
: Temperatura
final
6. Indicações gerais
6.1 Indicações para a minimização de erros
Supondo que as marcações de corrente e tensão sejam
suficientemente exatas, as duas fontes de erro
encontram-se na leitura da temperatura e na perda de
calor.
A perda de calor é dependente de quanto alta à
temperatura final se encontre acima da temperatura
do ambiente. Ela pode ser minimizada, em que, no
possível, o aumento de temperatura seja mantido
pequeno.
Quando a precisão de leitura do termômetro é de 1°
C, então resulta um erro relativamente grande de 10%
num aumento de temperatura em 10° C.
Por isso vale encontrar um equilíbrio entre o erro, que
é causado pela perda de calor num aumento de
temperatura muito acentuado, e do erro
relativamente grande na leitura de um aumento de
temperatura baixo.
Um aumento de temperatura em 20° C resulta numa
quota de erro de 5% (numa precisão de leitura do
termômetro de 1° C) e um erro relativamente
pequeno por perda de calor.
6.2 Evitação da perda de calor segundo Rumford
Segundo Rumford a perda de calor pode ser evitada
pelo seguinte processo. Se o calorímetro de cilindro
for guardado por algumas horas num refrigerador
antes da experiência, então a sua temperatura inicial
encontra-se por
θ abaixo da temperatura de
ambiente. Se a seguir a sua temperatura final está em
θ acima da temperatura de ambiente, então a
quantidade de calor recebida, enquanto a sua
temperatura está abaixo da temperatura de ambiente,
é igual à quantidade de temperatura que ele cede,
quando a sua temperatura está acima da temperatura
de ambiente. Então não dará lugar a nenhuma perda
de calor.
U33020
0...5 A 0...20 V
V A
0 0 0 4
.
2 0 1
.
Fig. 1 Montagem experimental