Meriam MANOMETERS - Manual (Page 2)

Density is a function of temperature and gravity is
a function of latitude and elevation. Because of this
relationship some ambient conditions must be selected as
standard so that pressure bears a fixed definition.
Standard conditions for mercury used as a unit of pressure:
Gravity: 980.665 cm/sec 2 (32.174 ft/sec 2 )
at sea level and 45.544 degrees latitude
Temperature: 0°C (32°F) density = 13.5951 g/cm 3
Standard conditions for water used as a unit of pressure.
Gravity: 980.665 cm/sec 2 (32.174 ft/sec 2 )
at sea level and 45.544 degrees latitude
Temperature: 4°C (39.2°F) density = 1 g/cm 3
Though it is recommended that the value of a water
column as a unit of pressure be at 4°C, its universal
acceptance has been slow. For instance in aeronautics
15°C (59°F) is used. The American Gas Association uses
15.56°C (60°F), and in orifice flowmeter work 20°C
(68°F) is commonly used.
Recognizing a manometer may be read outside, standard
temperature and gravity corrections can be applied to
improve the accuracy of a manometer reading at any given
conditions.
Fluid Density Corrections
Manometers indicate the correct pressure at only one
temperature. This is due to the fact that the indicating
fluid density changes with temperature. If water is the
indicating fluid, an inch scale indicates one inch of water
at 4°C only. On the same scale mercury indicates one
inch of mercury at 0°C only. If a reading using water or
mercury is taken at 20°C (68°F) then the reading is not an
accurate reading. The error introduced is about 0.4% of
reading for mercury and about 0.2% of reading for water.
Since most manometers are read at temperatures well
above the standard temperature, corrections are needed.
A simple way of correcting for the temperature error is to
ratio the densities.
(Standard) ρ
o
gh
o
= (Ambient) ρ
t
gh
t
h
o
= the corrected height of the indicating fluid to standard
temperature
h
t
= height of the indicating fluid at the temperature
when read
ρ
o
= density of the indicating fluid at standard temperature
ρ
t
= density of the indicating fluid at the temperature
when read
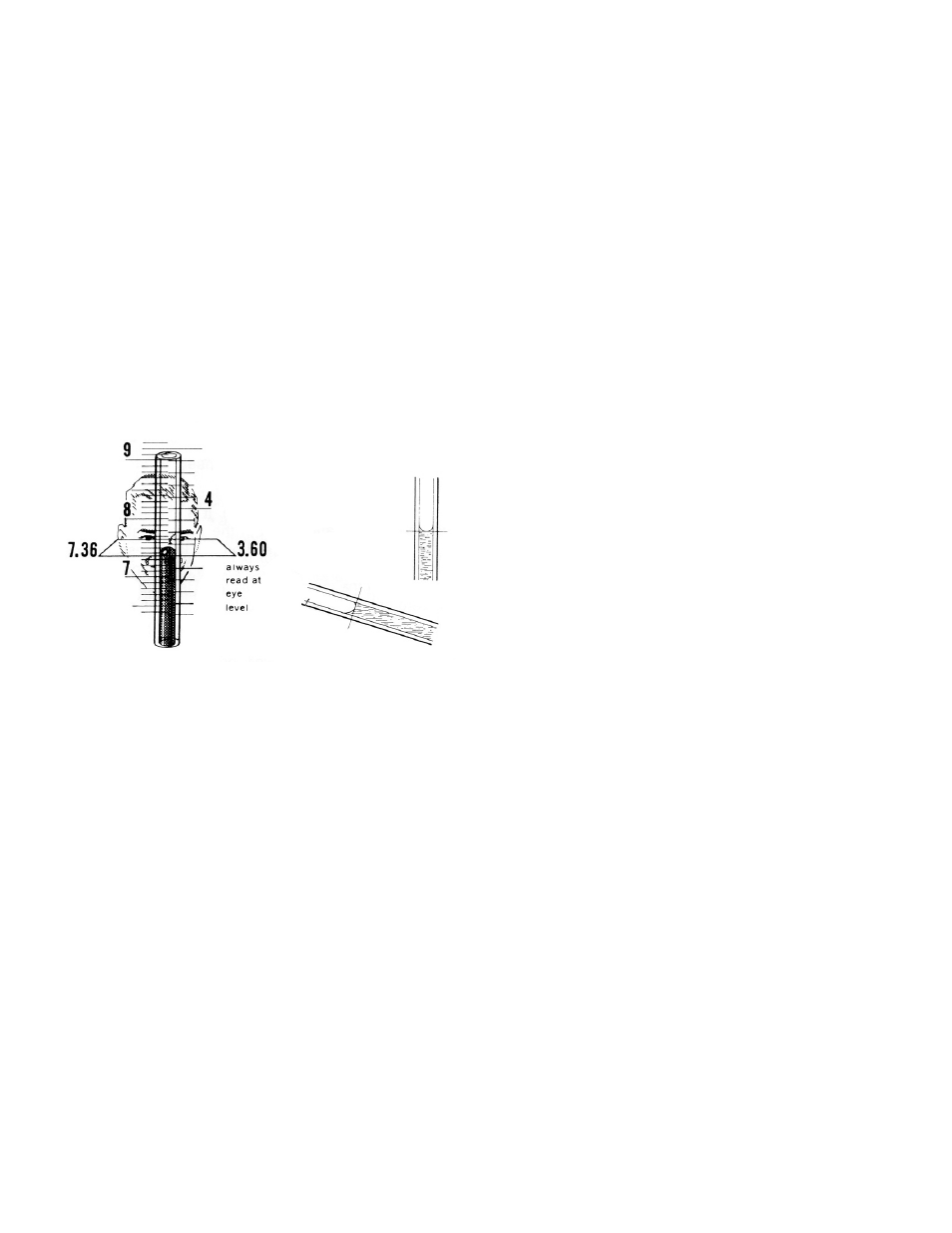
6. Reading
For consistent results, it is necessary that the fluid
meniscus always be observed in the same way. A
convex meniscus forms when mercury is used. In
this instance the fluid level should be observed from
the upper most point. For all other indicating fluids
a concave meniscus forms. The reading in this case
should be observed from the lowest point of the
meniscus. To duplicate factory calibration of incline
manometers, this technique needs to be followed.
It is important to remember the levels in both legs of
U-tube manometers must be read and these readings
added together to obtain an actual indication.
A plane tangent to the fluid meniscus and at a right
angle to the tube bore intercepts the scale where it
should be read.
7. Theory
The fundamental relationship for pressure expressed
by a liquid column is:
p = P
2
- P
1
= ρgh
p = differential pressure
P
1
= pressure applied to one liquid surface
P
2
= pressure applied to the other liquid surface
ρ = mass density of the liquid (specific gravity)
g = acceleration of gravity
h = height of the liquid column
In the case of absolute manometers (barometers), P
1
is equal to zero absolute pressure, simplifying the
equation to:
P = ρgh
As simple as manometry is, certain aspects are often
overlooked. Manometry incorporates both a value for
density and gravity. These two values are not constant.