Flowline LD32‐S4_1 DeltaSpan - Manual (Page 9)

Rev B MN301040 9 of 16
GETTING STARTED Step Seven
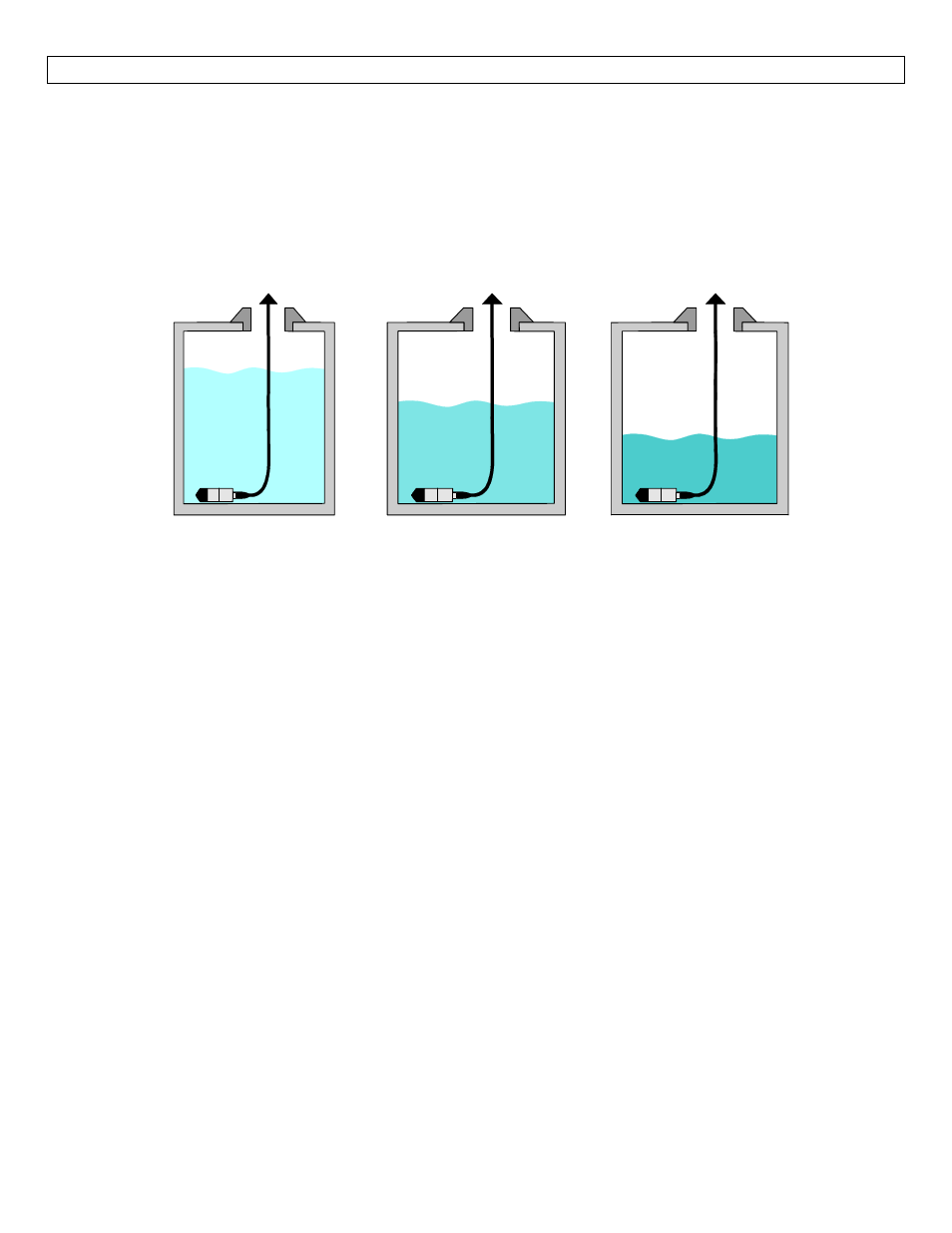
How does Specific Gravity affect pressure transmitters?
The Specific Gravity (SG) of a liquid will not change the pressure of the transmitter, but will affect how the
transmitter reads the liquid height. Remember, liquids with a SQ < 1.0 are lighter than water and liquids with
a SG > 1.0 are heavier than water.
 Water has a SG = 1.0.
 A SG < 1.0 requires more liquid (a taller water column) to equal the same pressure as with water.
 A SG > 1.0 requires less liquid (shorter water column) to equal the same pressure as with water.
SG = 0.9 SG = 1.0 SG = 1.2
To calculate the Maximum Liquid Height of a sensor, use the following formula:
Maximum Liquid Height (feet) = (Pressure Range x 2.31) / SG
Maximum Liquid Height (meters) = (Pressure Range x 0.704) / SG
Example: 15 psi transmitter installed in a liquid with a SG=0.9 will have a
Maximum Liquid Height = 38.5 feet (11.73 m) or [(15 psi x 2.31’/psi)/ 0.9 = 38.5’].
Note: The above formula will always provide the Maximum Liquid Height for any pressure transmitter.
Example: Compare the Maximum Liquid Height of a liquid with a SG = 0.9 to one with a SG = 1.0.
 SG = 0.9: a 15 psi transmitter will have a Maximum Liquid Height = 38.5’ (11.73 m)
 SG = 1.0: a 15 psi transmitter will have a Maximum Liquid Height = 34.65’ (10.56 m)
A change in SG of 0.1 will increase the Maximum Liquid Height of a transmitter by 3.83’ (1.2 m). Thus, when
the Specific Gravity is less than 1.0, the Maximum Liquid Height of the transmitter will increase.
The reverse is true by increasing the Specific Gravity. With a SG = 1.2, the Maximum Liquid Height = 28.88’
(8.80 m) with a 15 psi transmitter.
Maximum Liquid Height (28.88’) = (Pressure Range (15 psi) x 2.31) / SG (1.2)
Compare to a liquid with a SG = 1.0, the Maximum Liquid Height will decrease by 5.77’ (1.8 m). When the
Specific Gravity is greater than 1.0, the Maximum Liquid Height of the transmitter will decrease.
Note: Identifying the correct specific gravity for the fluid is critical in understanding the operational range of
the pressure transmitter.