Texas Instruments TI-85 User Manual
Page 24
B-24
TI-85/TI-86 Graphing Calculators
Copyright © Houghton Mifflin Company. All rights reserved.
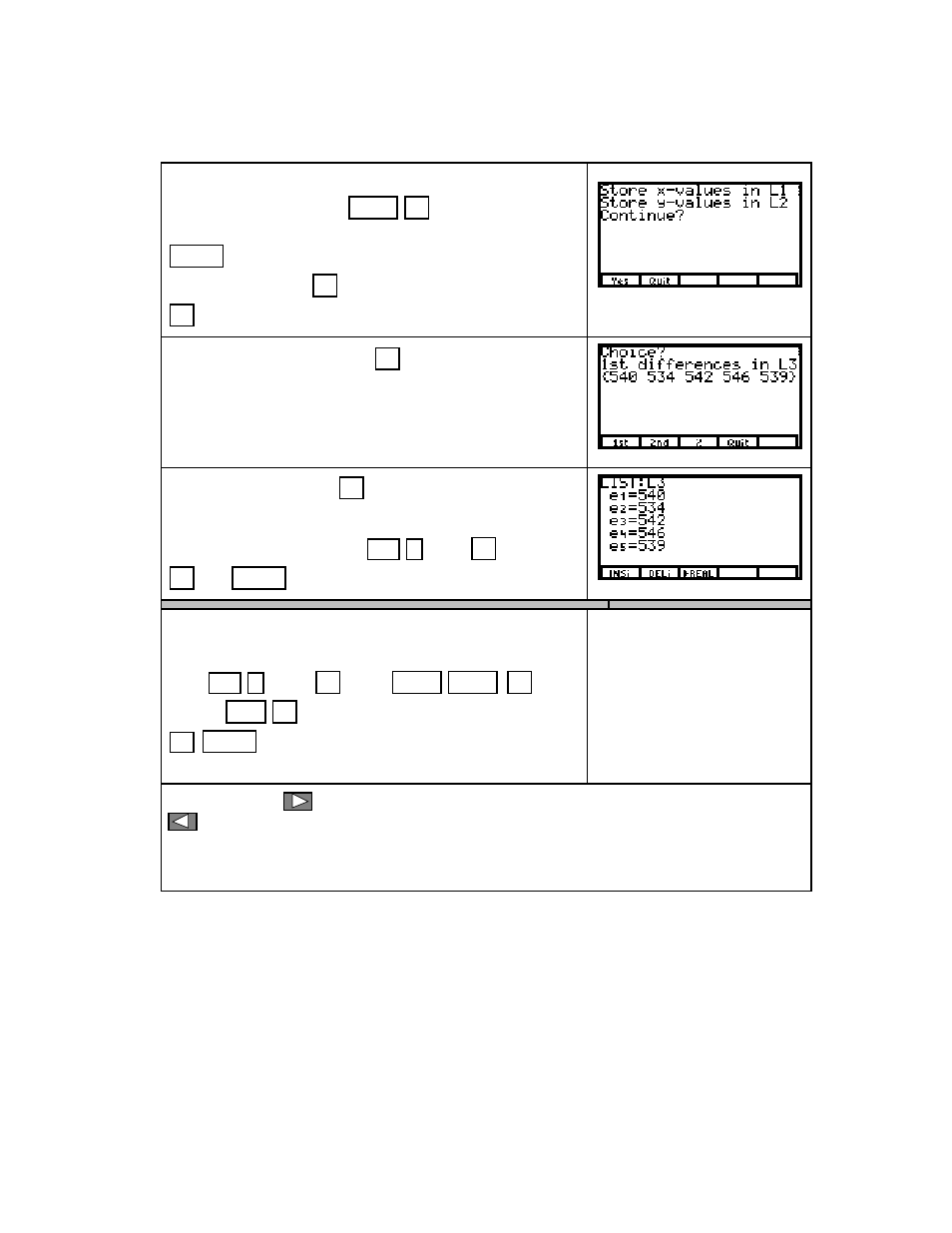
output values are constant. If the first differences are ÒcloseÓ to constant, this is an
indication that a linear model may be appropriate.
Program
DIFF
is given in the TI-85/TI-86 Appendix.
To run the program, press
PRGM
F1
(
NAMES
) and
then the
F
-key under the name of the program. Press
ENTER
. If you have not entered the data, stop the
program by pressing
F2
(
Quit
) . To continue, press
F1
(
Yes
) .
At the
Choice?
prompt, press
F1
(
1st
) to generate
the list of first differences.
Note: You may not be able to see the complete list
on this screen. If not, go to the list editor to see the
complete list of first differences stored in
L
3
.
Exit program
DIFF
with
F4
(
Quit
) .
TI-85
View list
L
3
containing the first differences in
the output data by pressing
2nd
–
(
LIST
)
F4
(
EDIT
)
F3
(
L3
)
ENTER
.
TI-86
If you do not want to use program
DIFF
, you can
use your TI-86 to compute first differences of any list.
Press
2nd
–
(
LIST
)
F5
(
OPS
)
MORE
MORE
F4
(
Deltal(
)
EXIT
F3
(
NAMES
) and the menu key under
L
2.
Press
)
ENTER
to see the list of first differences in
the output data.
If necessary, use
to scroll to the right to see the remainder of the first differences. Use
to scroll back to the left.
Be certain you have evenly-spaced input values if you are using this to give information
about first differences and linear models.
¥ Both Program
DIFF
should not be used for data with input (
L
1
) values that are not evenly
spaced. First differences give no information about a possible linear fit to data with
inputs that are not the same distance apart.
1.4.7 FINDING A LINEAR MODEL
Use your calculator to obtain the linear model t h a t
best fits the data. Your calculator can find two different, but equivalent, forms of the linear
model: y = ax + b or y = a + bx. For convenience, we always choose the model y = ax + b.
