Texas Instruments TI-85 User Manual
Page 15
Chapter 1
B-15
Copyright © Houghton Mifflin Company. All rights reserved.
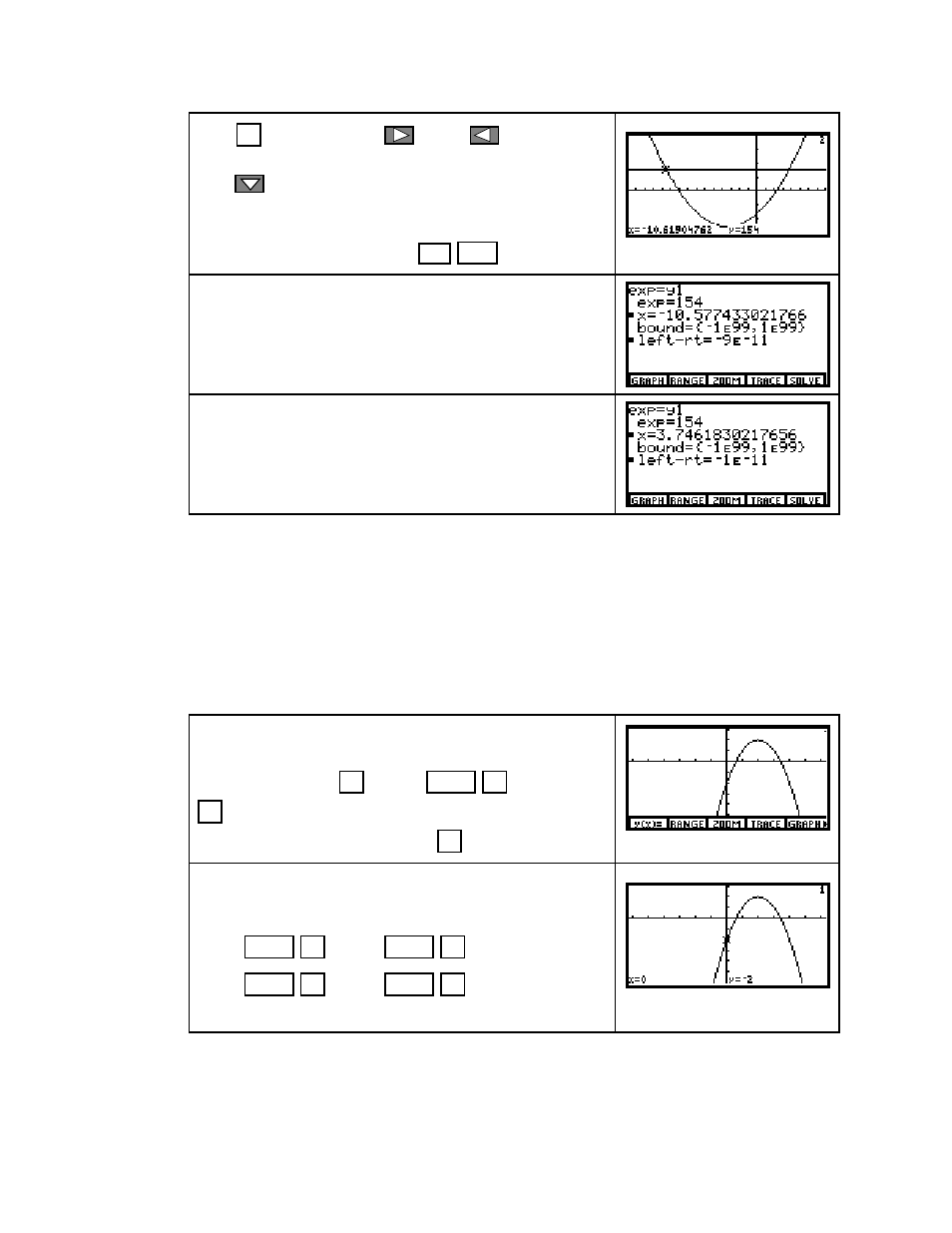
Press
F4
(
TRACE
) and use
and/or
to move
along the graph of the equation in
y
1
.
Press
to jump from the graph of
y
1
to the graph of
y
2
. Tracing reveals that guesses for the input values
where these two graph intersect are
x
»
–
10.6
,
x
»
3.8
.
Return to the home screen with
2nd
EXIT
(
QUIT
) .
Access the
SOLVER
and enter the equation
y
1
=
y
2
as shown on the right. Enter the guess for the left-
most intersection point and solve for x.
Enter the guess for the rightmost intersection point
and solve for x.
The two solutions to the equation, reported to four
decimal places, are x =
–
10.5774 and x = 3.7462.
1.2.3 GRAPHICALLY FINDING INTERCEPTS
Finding where a function graph crosses
the vertical and horizontal axis can be done graphically as well as by the methods
indicated in 1.2.2 of this Guide. Remember the process by which we find intercepts:
¥ To find the y-intercept of a function y = f(x), set x=0 and solve the resulting equation.
¥ To find the x-intercept of a function y = f(x), set y=0 and solve the resulting equation.
Also remember that an x-intercept of a function y = f(x) has the same value as the root or
solution of the equation f(x) = 0.
Clear all locations in the
y(x)=
list and enter in
y
1
f(x) = 4x Ð x
2
Ð 2.
Draw a graph with
F3
(
ZOOM
)
MORE
F4
(
ZDECM
) . Press
F2
(
RANGE
or
WIND
) and reset
yMin
to -
6
for a
good view of all intercepts. Press
F5
(
GRAPH
) .
Even though it is very easy to find f(0) =
–
2, you can
have the calculator find the y-intercept while view-
ing the graph by pressing
TI-85
MORE
F1
(
MATH
)
MORE
F4
(
YICPT
)
TI-86
MORE
F1
(
MATH
)
MORE
F2
(
YICPT
)
Both
View the y-intercept f(0) =
–
2.
