Scotch Brand 5.1.10 - Manual (Page 53)

edgenbr
vlbltab
verttab
velotab
vendtab
vnodnbr
velmbas
vnodbas
velmnbr
edgetab
24
11 10 11
5 9 25 13 14 16 18 20 21 22 23 1
1 4
2
5
1
6
3
5 7 6 5 4 6 7 8 9 2 2 1 3 1 1 3 3 3 2 2 1
4
8
3
10
11
7
8 9
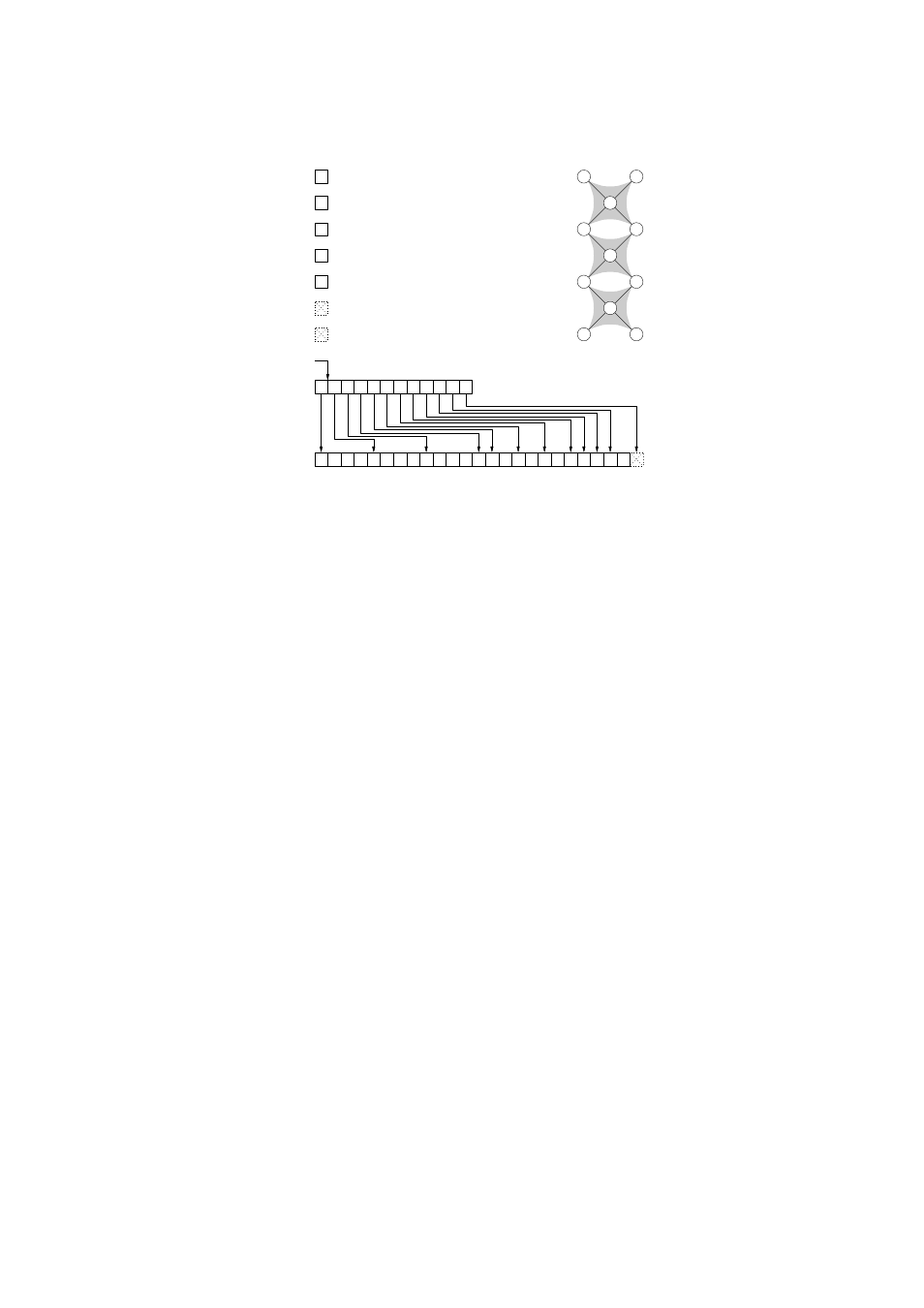
Figure 18: Sample mesh and its description by libScotch arrays using a compact
edge array. Numbers within vertices are vertex indices. Since the edge array is
compact, verttab is of size vertnbr + 1 and vendtab points to verttab + 1.
vendtab
Array of after-last indices in edgetab of vertex adjacency sub-arrays. For
any element or node vertex i, with baseval ≤ i < (baseval + vertnbr),
vendtab[i]
− verttab[i] is the degree of vertex i, and the indices of the
neighbors of i are stored in edgetab from edgetab[verttab[i]] to edgetab
[vendtab[i]
−1], inclusive.
When all vertex adjacency lists are stored in order in edgetab, it is possible to
save memory by not allocating the physical memory for vendtab. In this case,
illustrated in Figure 18, verttab is of size vertnbr + 1 and vendtab points to
verttab
+ 1. This case is referred to as the “compact edge array” case, such
that verttab is sorted in ascending order, verttab[baseval] = baseval and
verttab[baseval
+ vertnbr] = (baseval + edgenbr).
velotab
Array, of size vertnbr, holding the integer load associated with each vertex.
As for graphs, it is possible to handle elegantly dynamic meshes by means of the
verttab and vendtab arrays. There is, however, an additional constraint, which is
that mesh nodes and elements must be ordered consecutively. The solution to fulfill
this constraint in the context of mesh ordering is to keep a set of empty elements
(that is, elements which have no node adjacency attached to them) between the
element and node arrays. For instance, Figure 19 represents a 4-element mesh
with 6 nodes, and such that 4 element vertex slots have been reserved for new
elements and nodes. These slots are empty elements for which verttab[i] equals
vendtab[i]
, irrespective of these values, since they will not lead to any memory
access in edgetab.
Using this layout of vertices, new nodes and elements can be created by growing
the element and node sub-arrays into the empty element sub-array, by both of
its sides, without having to re-write the whole mesh structure, as illustrated in
Figure 20. Empty elements are transparent to the mesh ordering routines, which
base their work on node vertices only. Users who want to update the arrays of
53