3B Scientific Fine Beam Tube T User Manual
Electricity, Fine beam tube
Electricity
Cathode ray tubes
1 / 4
Fine beam tube
DETERMINE THE SPECIFIC CHARGE OF AN ELECTRON
• Demonstrate the deflection of electrons in a uniform magnetic field along a closed circular path
• Determine the Helmholtz coil current I
H
in relation to the accelerating voltage U of an electron gun where the electrons
are moving in a circular path of constant radius r
• Determine the specific charge of an electron e/m from the measurements
UE307070
08/06 UK
BASIC PRINCIPLES
In the fine beam tube, the electrons move along a circular
path in a uniform magnetic field. The tube contains neon
gas at a precisely set pressure. The gas atoms are ionised
along the length of the circular path due to collisions with
electrons. As a result, they are excited and emit light,
thereby indirectly making the circular path of the elec-
trons visible. The radius of the path can then be meas-
ured directly with a ruler. Since the accelerating voltage U
of the electron gun and the magnetic field B are known, it
is possible to calculate the specific charge of an electron
e/m from the radius of the circular path r.
An electron moving with velocity v in a direction perpendicu-
lar to a uniform magnetic field B experiences a Lorentz force
in a direction perpendicular to both the velocity and the
magnetic field.
B
v
e
F
⋅
⋅
=
(1)
e: elementary charge
This gives rise to a centripetal force on the electron in a cir-
cular path with radius r, where
r
v
m
F
2
⋅
=
and
(2)
m is the mass of an electron.
Thus,
r
v
m
B
e
⋅
=
⋅
(3)
The velocity
v depends on the accelerating voltage of the
electron gun:
U
m
e
v
⋅
⋅
= 2
(4)
Therefore, the specific charge of an electron is given by:
( )
2
2
B
r
U
m
e
⋅
⋅
=
(5)
If we measure the radius of the circular orbit in each case for
different accelerating voltages
U and different magnetic
fields B, then, according to equation 5, the measured values
can be plotted in a graph of r
2
B
2
against
2U as a straight line
through the origin with slope e/m.
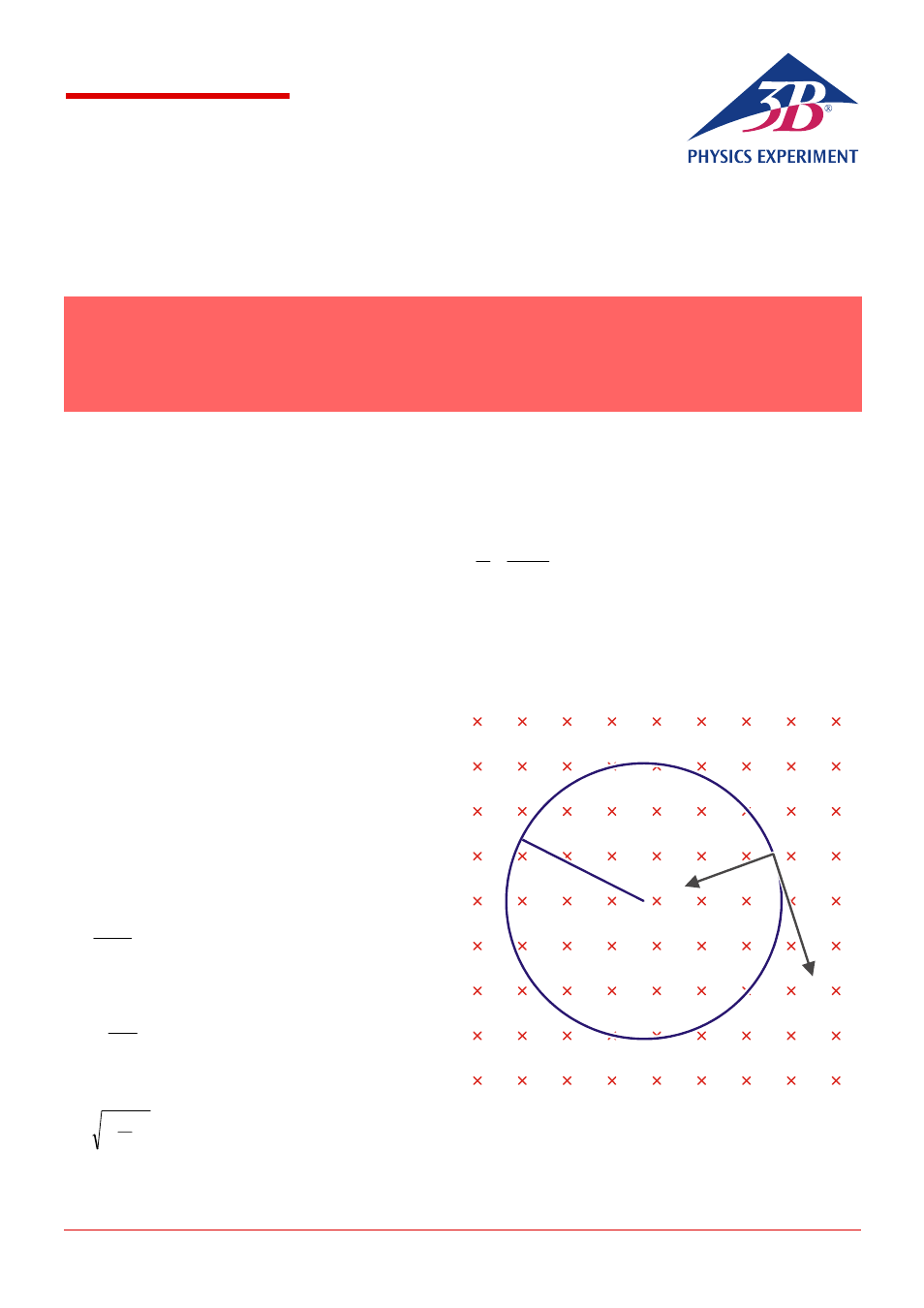
B
F
v
r
Fig. 1:
Deflection of electrons moving with velocity v in a magnetic
field B by a Lorentz force F along a closed circular path of
radius r
