3B Scientific Teltron Critical Potentials Tube S with He-Filling User Manual
Atomic and nuclear physics, Critical potentials, Atomic shells
Atomic and Nuclear Physics
Atomic Shells
1 / 3
Critical Potentials
DETERMINE THE CRITICAL POTENTIALS OF A HELIUM ATOM.
• Measure the collector current I
R
as a function of the accelerating voltage U
A
.
• Compare the positions of the current maxima with the known critical potentials of the helium atom.
• Identify the doublet structure in the term scheme of helium (ortho and para helium).
UE502050
08/08 JS
BASIC PRINCIPLES
The expression “critical potential” is a general name for all the
excitation and ionisation energies in the electron shells of an
atom. The corresponding electronic states of the atom can be
excited in various ways, for example by inelastic collisions with
electrons. If the kinetic energy of the electron corresponds
exactly to a critical potential, the electron can transfer all its
kinetic energy to the atom in an inelastic collision. Using an
experiment set-up originally designed by Gustav Hertz, this
effect can be used to determine the critical potentials.
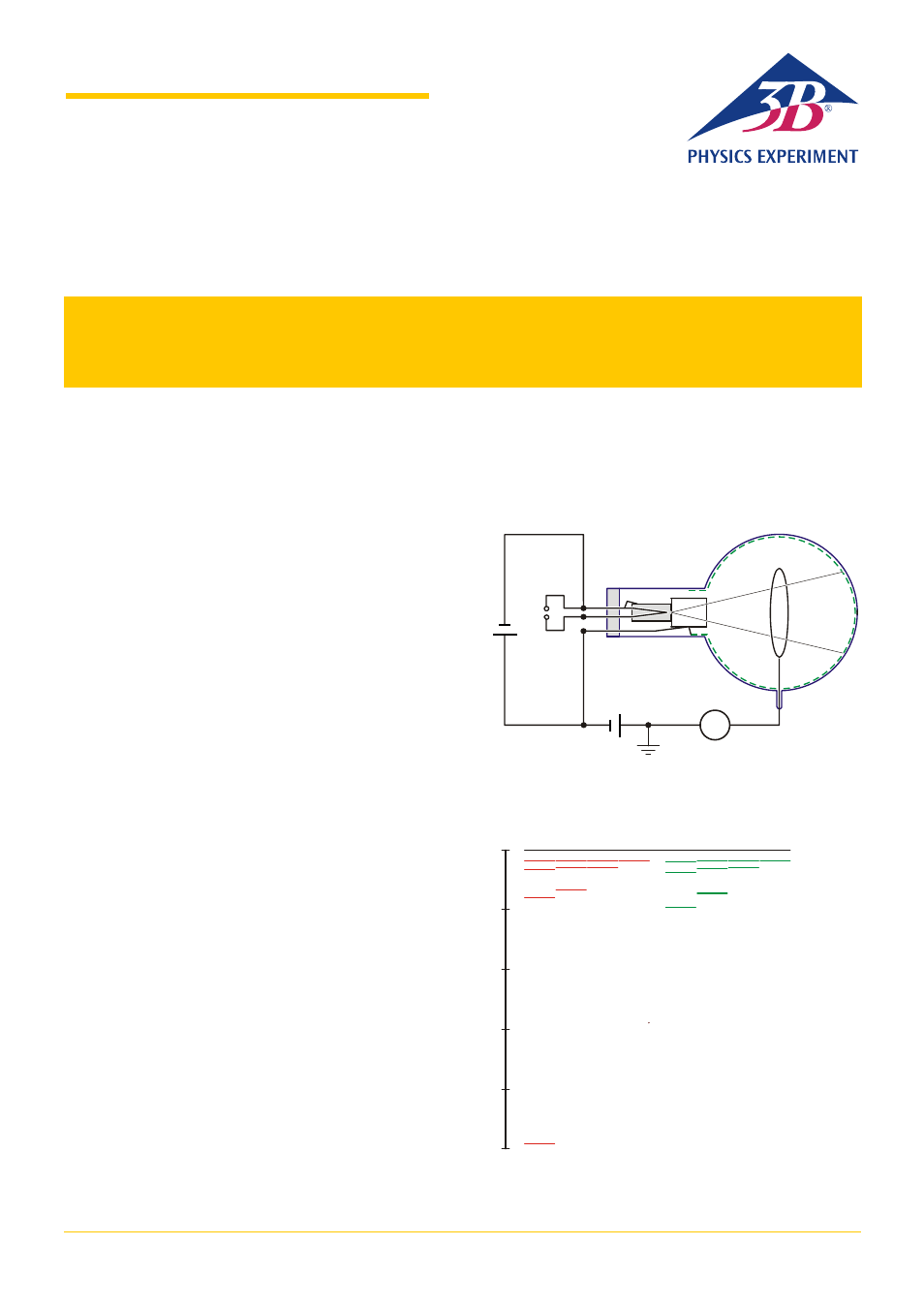
In a tube that has been evacuated and then filled with helium, free
electrons are accelerated by a voltage U
A
to form a divergent beam
passing through a space at a constant potential. To prevent the
walls of the tube becoming charged, the inner surface is coated
with a conducting material and connected to the anode A (see Fig.
1). In the tube there is a ring-shaped collector electrode R, through
which the divergent beam can pass without touching it, even
though the ring is at a slightly higher potential.
However, a small current I
R
, with a value in the order of
picoamperes, is measured at the collector ring, and is found to
depend on the accelerating voltage U
A
. It shows characteristic
maxima, which are caused by the fact that the electrons can
undergo inelastic collisions with helium atoms during their passage
through the tube. The kinetic energy E of an electron is as follows:
(1)
A
U
e
E
⋅
=
e: elementary electron charge
If this energy corresponds exactly to a critical potential of the
helium atom, all the kinetic energy may be transferred to the
helium atom. In this instance the electron can then be attracted
and collected by the collector ring, thus contributing to an
increased collector current I
R
.
As the accelerating voltage is increased, successively higher levels of
the helium atom can be excited (see the term scheme of the helium
atom shown in Fig. 2), until finally the kinetic energy of the electron
is enough to ionise the helium atom. As the accelerating voltage is
increased further, the collector current shows a steady increase.
U
A
C
A
R
U
F
1.5 V
pA
Fig. 1: Schematic diagram of critical potential tube
0
E / eV
S = 0
S = 1
1
S
3
S
1
P
3
P
1
D
3
D
1
F
3
F
1
2
2
3
3
4
4
-5
-15
-10
-20
-25
Fig. 2: The term scheme of helium
red: total spin S = 0 (para helium),
green: total spin S = 1 (ortho helium)
