3B Scientific Metal Block Calorimeters - Manual (Page 2)

3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com
Subject to technical amendment
© Copyright 2008 3B Scientific GmbH
• Before starting the experimental run, wait for a
few minutes before taking the temperature of the
calorimeter block.
• Switch on the heater and start the clock.
• Wait until the temperature has risen about 20 o C
and record the time and final temperature.
The specific heat capacity can then be calculated from
the equation:
( )
1 2
θ − θ ⋅ ⋅ = ⋅ ⋅
c m t U I
with I: current, U: voltage, t: time, m: mass of calori-
meter block, c: specific heat capacity,
θ
1
: initial
temperature,
θ
2
: final temperature
6. General notes
6.1 Explanation of how to minimise the error
Assuming that the readings for the current and voltage
are reasonable accurate, the two main sources of error
in the experiment will be the readings of the
temperature change and the effects of any heat loss.
Obviously the heat loss will depend on the excess
temperature above the room temperature, so this can
be minimised by keeping the temperature rise as
small as possible.
If the thermometer can only be read accurately to 1 o ,
then a temperature rise of 10 o would give a 10% error,
which is really too large for this type of experiment.
Therefore, it is a balance between the error
introduced by a large temperature increase causing
heat losses, and a small temperature increase giving a
large percentage error in the temperature readings. A
20
o rise in temperature will give a 5% error in reading
the thermometer (assuming it can only be read
accurately to 1
o ) and a reasonable low error due to
heat loss.
6.2 Rumford’s correction
Rumford argued that heat losses could be eliminated
by the following process. If the metal block is kept in a
fridge for several hours before the experiment, then it
will start at, say,
θ below room temperature. If its final
temperature after the experiment was
θ above room
temperature, then the heat it took in while below
room temperature would be equal to the heat it gave
out while above room temperature, so there would be
no heat loss.
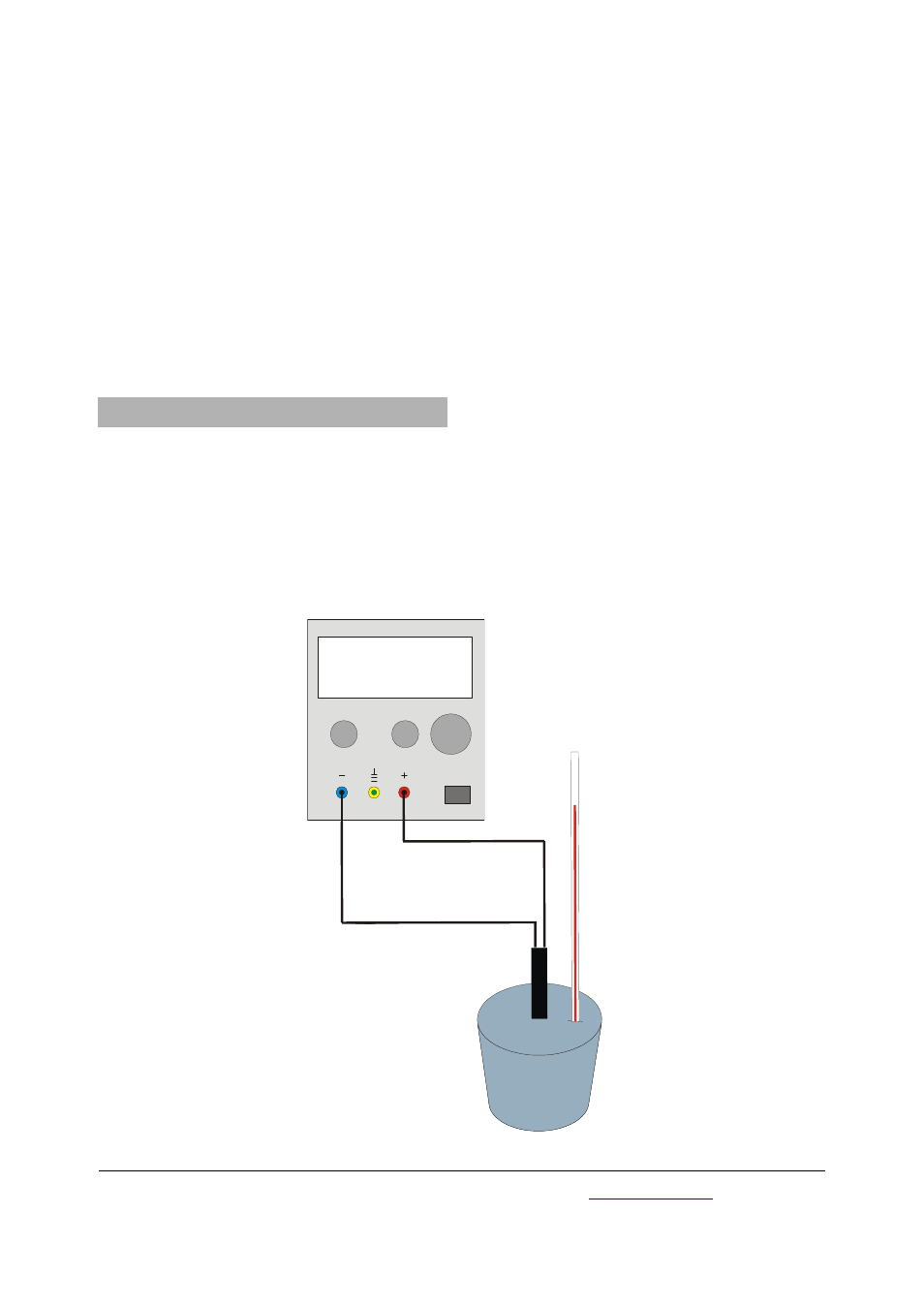
U33020
0...5 A 0...20 V
V A
0 0 0 4
.
2 0 1
.
Fig. 1 Experimental set up